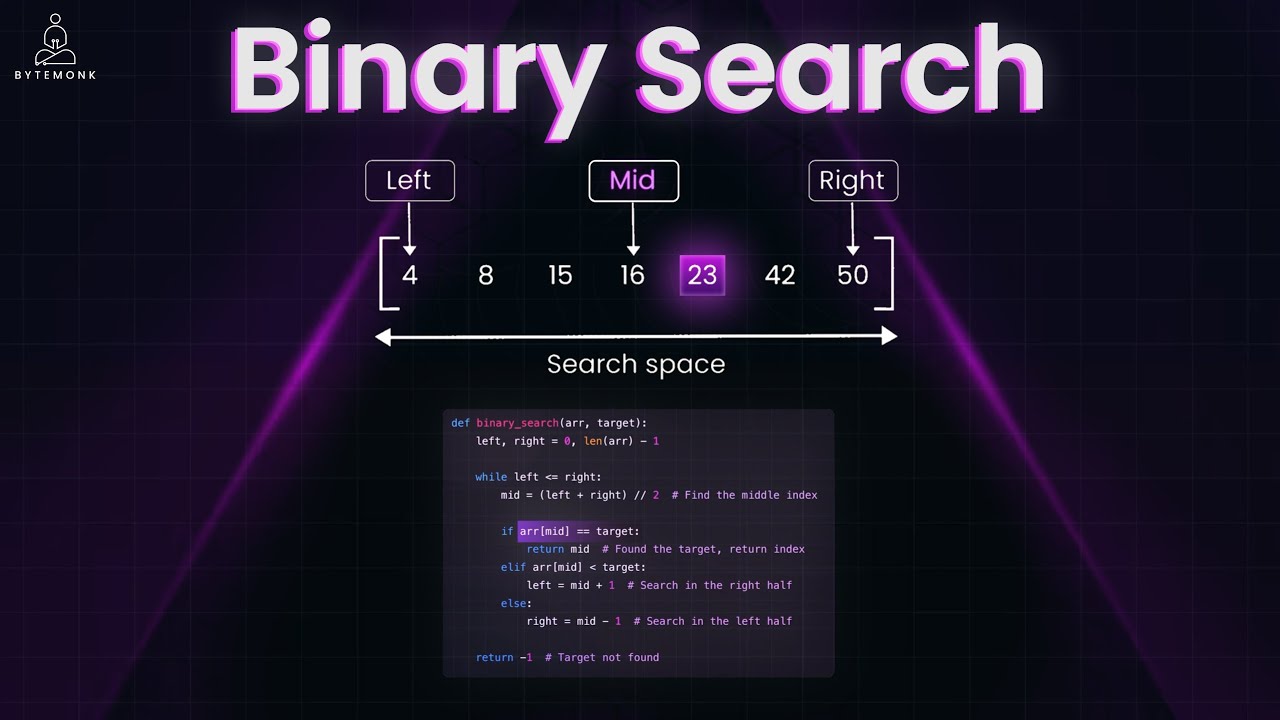
Searching is one of the most common operations in computer science, and binary search stands as one of the most powerful algorithms in a developer's toolkit. Unlike linear search that scans through items one by one, binary search divides the search space in half with each step, making it exponentially faster for sorted data collections.
How Binary Search Works: A Visual Explanation
To understand binary search, let's start with a simple example. Imagine we have a sorted array of numbers, and we need to find a specific value like 23.
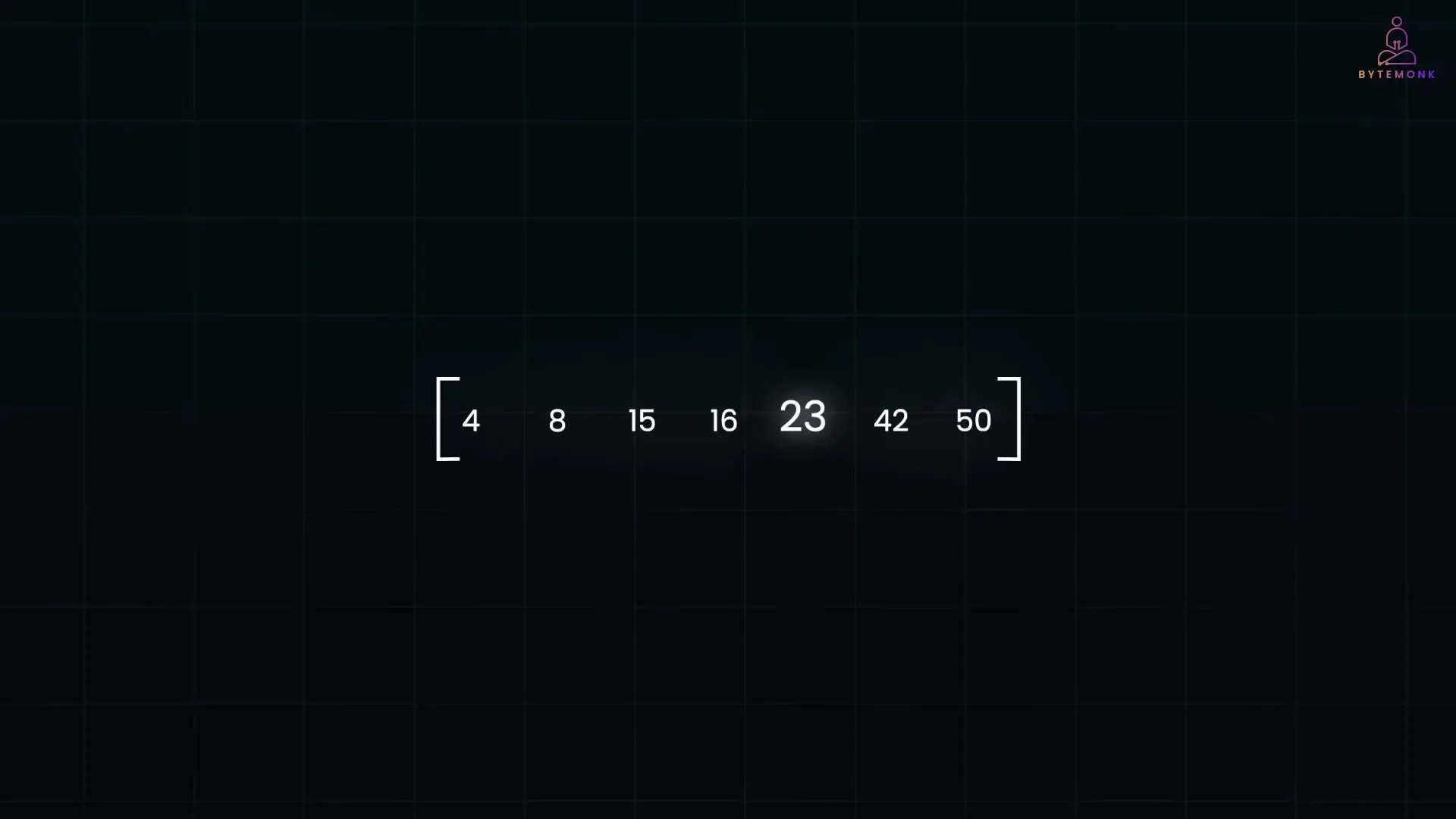
With linear search, we would check each element sequentially from the beginning until we find 23 or reach the end. This approach works but becomes inefficient for large datasets, especially if our target is near the end.
Binary search takes advantage of the array being sorted by using a divide-and-conquer approach:
- Start by examining the middle element of the array
- If this element equals our target, we're done
- If the middle element is smaller than our target, ignore the left half and search in the right half
- If the middle element is larger than our target, ignore the right half and search in the left half
- Repeat the process on the remaining half until we find the target or run out of elements
In our example, the middle element is 16, which is smaller than 23, so we ignore the left half. The new middle of the remaining right half is 42, which is greater than 23, so we ignore the right portion. Finally, the middle of the remaining section is 23 itself—we found it! With each step, we eliminated half of the remaining elements, making the search extremely efficient.
Binary Search Implementation in Python
Here's how binary search looks in Python code:
def binary_search(array, target):
left = 0
right = len(array) - 1
while left <= right:
mid = (left + right) // 2
# Check if target is present at mid
if array[mid] == target:
return mid
# If target is greater, ignore left half
elif array[mid] < target:
left = mid + 1
# If target is smaller, ignore right half
else:
right = mid - 1
# Target is not present in the array
return -1The time complexity of binary search is O(log n), which is significantly better than the O(n) complexity of linear search. This logarithmic efficiency makes binary search incredibly valuable for large datasets.
Advanced Application: Searching in a Rotated Sorted Array
Binary search can be adapted for more complex scenarios. Consider a rotated sorted array—an array that was initially sorted but then rotated at some pivot point. For example, [15, 16, 19, 20, 25, 1, 3, 4, 5, 7, 10, 14] was originally sorted as [1, 3, 4, 5, 7, 10, 14, 15, 16, 19, 20, 25] but rotated at index 5.
To search efficiently in such an array, we need to modify our binary search approach:
- Find the middle element
- Determine which half (left or right) is sorted
- Check if the target is within the range of the sorted half
- If yes, search in that half; otherwise, search in the other half
- Repeat until the target is found or the search space is empty
def search_rotated_array(array, target):
left = 0
right = len(array) - 1
while left <= right:
mid = (left + right) // 2
# Found target
if array[mid] == target:
return mid
# Check which half is sorted
if array[left] <= array[mid]: # Left half is sorted
# Check if target is in the sorted left half
if array[left] <= target < array[mid]:
right = mid - 1
else:
left = mid + 1
else: # Right half is sorted
# Check if target is in the sorted right half
if array[mid] < target <= array[right]:
left = mid + 1
else:
right = mid - 1
return -1 # Target not foundThis modified binary search still maintains the O(log n) time complexity, demonstrating the algorithm's versatility and power.
Real-World Applications of Binary Search
Binary search isn't just a theoretical concept or an interview question—it's a fundamental algorithm with numerous practical applications:
1. Computing Square Roots
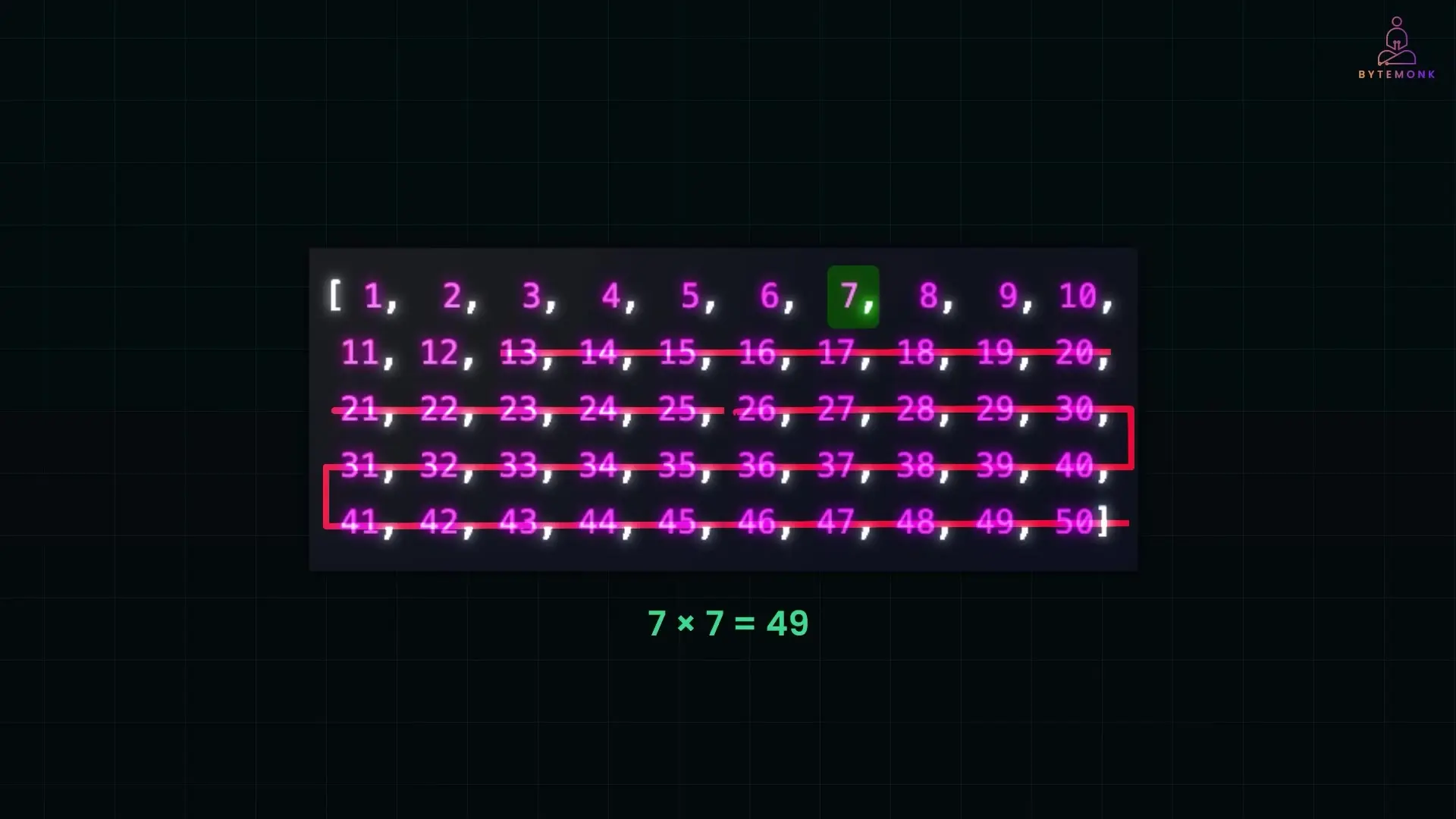
Binary search can be used to efficiently compute square roots without using built-in functions. For example, to find the square root of 50:
- We know the answer is between 1 and 50
- Start with the middle: 25. Square it: 625. Too high!
- Try the middle of 1 and 25: 13. Square it: 169. Still too high!
- Try the middle of 1 and 13: 7. Square it: 49. Very close!
def square_root(n, precision=0.0001):
if n < 0:
return None # No real square root for negative numbers
if n == 0 or n == 1:
return n
left = 0
right = n
while right - left > precision:
mid = (left + right) / 2
mid_squared = mid * mid
if mid_squared == n:
return mid
elif mid_squared < n:
left = mid
else:
right = mid
return (left + right) / 2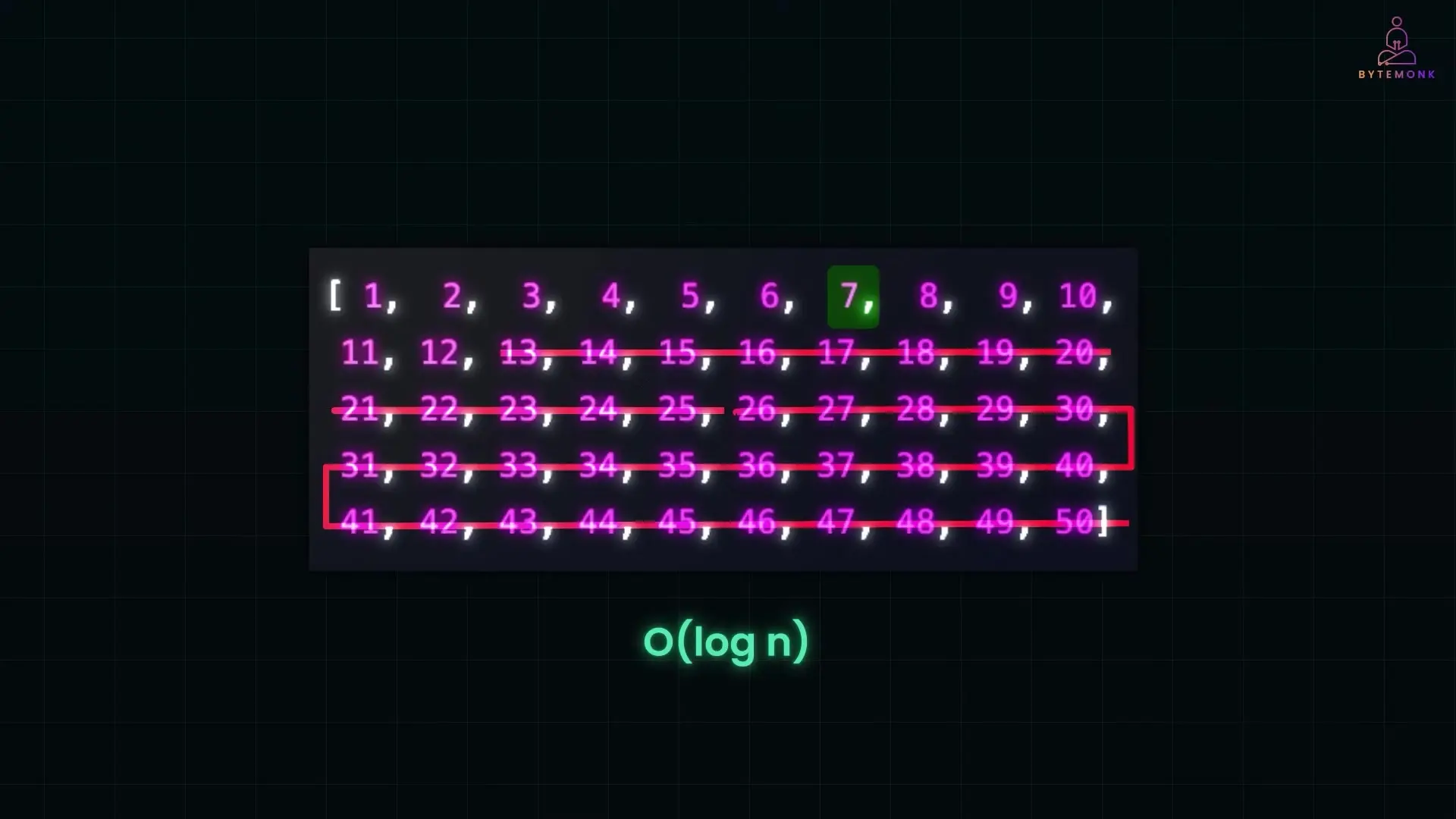
2. Database Systems
Relational databases like MySQL and PostgreSQL use B-trees (a variation of binary search) for indexing. This is why searching for specific records in databases with millions of entries can be lightning-fast—binary search principles allow the database to quickly narrow down where the data might be stored.
3. Search Engines
When you type a query into a search engine, it doesn't scan billions of web pages sequentially. Instead, search engines use inverted indices and binary search-based techniques to retrieve relevant results in milliseconds.
4. Machine Learning
Binary search is used in training machine learning models, particularly for hyperparameter optimization. When tuning parameters like learning rate, a binary search approach can help find optimal values more efficiently than grid search.
5. Computer Graphics
In computer graphics, binary search is used for operations like ray tracing and collision detection, helping to quickly locate where objects intersect in 3D space.
Why Binary Search Matters for Software Engineers
Understanding binary search isn't just about passing technical interviews—it represents a fundamental way of thinking about efficiency and optimization in software development. The divide-and-conquer approach teaches us to:
- Look for opportunities to eliminate large portions of work with each step
- Recognize when data structure organization (like sorting) can enable more efficient algorithms
- Think logarithmically rather than linearly when dealing with large datasets
- Apply the same principles to various problem domains beyond simple array searching
Conclusion
Binary search is a powerful algorithm that demonstrates how clever approaches can dramatically improve performance. By cutting the search space in half with each step, it achieves logarithmic time complexity—making it suitable for applications dealing with massive datasets. Whether you're building a database, optimizing a search function, or solving complex computational problems, understanding binary search and knowing when to apply it will make you a more effective software engineer.
The next time you face a problem that involves searching or optimization, consider whether binary search principles might offer an elegant solution. It's not just an algorithm—it's a way of thinking that can transform how you approach software development challenges.
Let's Watch!
Binary Search Algorithm: How It Works and Real-World Applications
Ready to enhance your neural network?
Access our quantum knowledge cores and upgrade your programming abilities.
Initialize Training Sequence