How Domino Logic Gates Model Computer Circuits: A Fascinating Step-by-Step Explanation

Have you ever wondered how computers actually process information at their most fundamental level? While modern computers use electricity flowing through microscopic circuits, we can actually model these same principles using something as simple as dominoes. By arranging dominoes in specific patterns, we can create physical representations of the logic gates that form the building blocks of all computer systems.

The Fundamental Concept: Representing Binary with Dominoes

At their core, computers operate using binary - a system of ones and zeros. In electronic circuits, these values are represented by the presence or absence of electrical current. With domino logic gates, we can model this same concept physically:

• A standing domino represents a 0 (absence of electricity/signal)
• A falling domino represents a 1 (presence of electricity/signal)
• The chain reaction of falling dominoes represents the flow of electricity through a circuit

This simple representation allows us to build physical models of the same logical operations that power digital devices. By carefully designing the paths and interactions of these falling dominoes, we can create functional logic gates - the fundamental building blocks of computation.

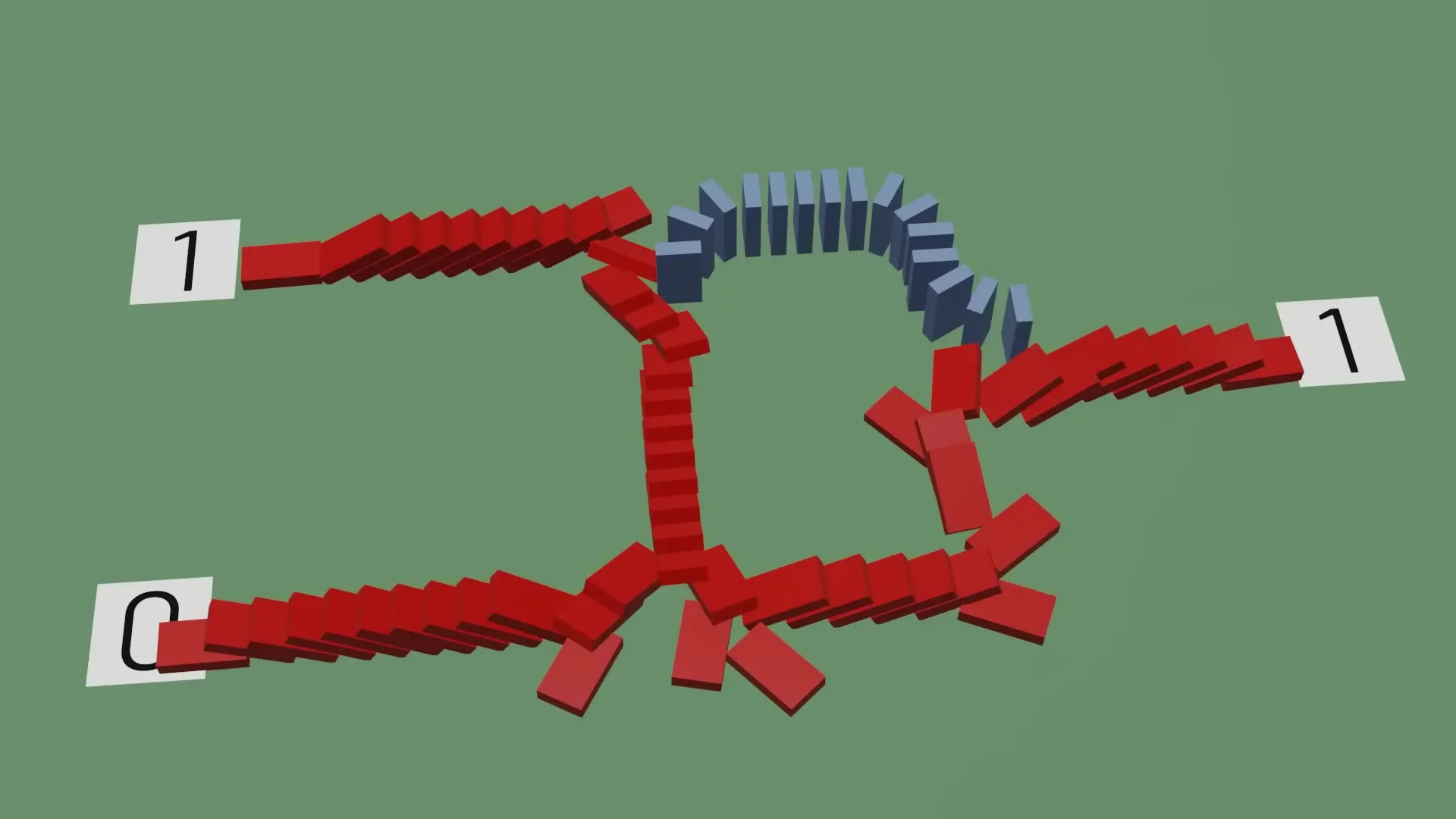
Building Basic Logic Gates with Dominoes

Logic gates are the fundamental processing units in computers that perform logical operations on binary inputs. Let's explore how to build three essential logic gates using domino arrangements.

The OR Gate with Dominoes

An OR gate produces a 1 output if either of its inputs (or both) is 1. With logic gates with domino's, this is straightforward to implement. We simply connect two input paths to a single output path:

• If neither input domino falls (both inputs are 0), the output domino remains standing (output is 0)
• If either input domino falls (either input is 1), it triggers the output domino to fall (output is 1)
• If both input dominoes fall (both inputs are 1), the output domino still falls only once (output is 1)

The Exclusive OR (XOR) Gate with Dominoes

The XOR gate is more complex - it outputs 1 only when exactly one input is 1, but outputs 0 if both inputs are 1. This requires a clever domino arrangement:

To create an XOR gate with domino logic gates, we design two input paths that cross each other. When only one input is triggered, the dominoes follow their path to the output. However, when both inputs are triggered simultaneously, the falling dominoes from each path collide with each other and stop, preventing either path from reaching the output.

• If neither input is 1, no dominoes fall and the output remains 0
• If exactly one input is 1, its dominoes fall along their path to trigger the output (producing a 1)
• If both inputs are 1, the falling dominoes from each path collide and stop, never reaching the output (producing a 0)

The AND Gate with Dominoes

An AND gate outputs 1 only when both inputs are 1. This requires a more sophisticated arrangement of logic gates with domino's that leverages the concept of interruption:

We create a primary input path with a long route to the output. Then we add a shorter branch that can interrupt this main path. Finally, we add a second input that can interrupt the interrupting path. This creates a system where both inputs must be 1 (falling) for the output to be 1.

• If neither input is 1, no dominoes fall and the output remains 0
• If only the first input is 1, its interrupting path blocks the main path, preventing the output from being 1
• If only the second input is 1, nothing happens to the output (remains 0)
• If both inputs are 1, the second input interrupts the interrupting path, allowing the main path to reach the output (producing a 1)

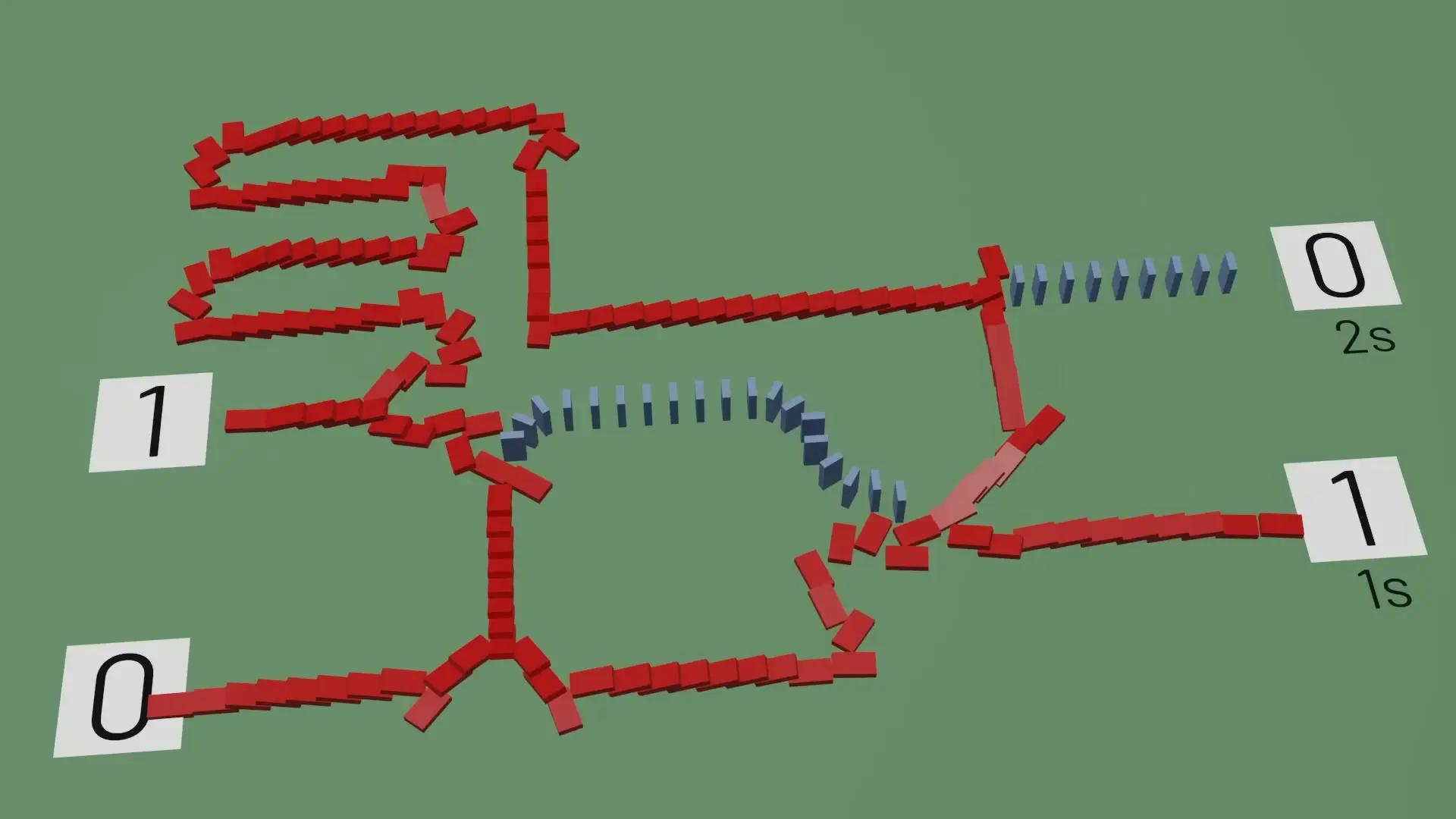
Building Adder Circuits with Domino Logic Gates

Now that we understand how to build basic logic gates with dominoes, we can combine them to create more complex circuits that perform actual computations. One of the most fundamental computational circuits is the binary adder.

The Half Adder: Adding Two Bits

A half adder adds two single binary digits and produces two outputs: a sum and a carry. This circuit can be constructed by combining an XOR gate and an AND gate:

• The XOR gate determines the ones place of the result (0+0=0, 0+1=1, 1+0=1, 1+1=0)
• The AND gate determines the carry or two's place (only 1+1 produces a carry of 1)

Using our domino logic gates, we can physically construct this half adder circuit. When neither input is triggered, both outputs remain 0. When exactly one input is triggered, the ones place output becomes 1. When both inputs are triggered, the ones place output remains 0 (due to the XOR collision), but the two's place output becomes 1.

The Full Adder: Adding Three Bits

To add larger numbers, we need a full adder, which adds three bits: two input bits plus a carry bit from a previous addition. A full adder can be constructed by combining two half adders and an OR gate.

With domino logic gates, this requires careful planning of path lengths to ensure proper timing of the interruptions and collisions. The resulting circuit can add any two binary numbers by processing one bit position at a time and passing the carry to the next position.

From Dominoes to Digital Computing

These domino arrangements demonstrate the same logical principles that govern modern computers. While computers use electricity instead of gravity and operate at much faster speeds, the underlying logic is identical:

• Basic logic gates (OR, XOR, AND) form the building blocks
• These gates combine to create functional units like adders
• Multiple adders work together to perform complex calculations
• The same principles scale up to perform any computation

The beauty of domino logic gates is that they make visible the invisible processes happening inside our computers. By watching dominoes fall along carefully designed paths, we can literally see computation happening before our eyes.

Practical Applications and Learning Opportunities

Beyond being a fascinating demonstration, building domino logic gates offers practical benefits for understanding computer science fundamentals:

1. Educational tool for teaching binary logic and circuit design
2. Visualization aid for abstract computing concepts
3. Hands-on introduction to hardware principles without electronic components
4. Demonstration of how complex behaviors emerge from simple rules

By constructing these physical models, students and enthusiasts can develop an intuitive understanding of the principles that power all digital devices, from smartphones to supercomputers.

Conclusion

From simple domino arrangements to complex computational circuits, we've seen how the fundamental principles of computing can be modeled physically. Domino logic gates provide a tangible representation of the abstract processes happening inside our computers, making visible the invisible world of digital logic.

While modern computers operate at speeds and scales far beyond what's possible with physical dominoes, the underlying logical principles remain the same. By understanding how domino logic gates work, we gain insight into the foundations of all digital technology.

The next time you use a computer, remember that beneath the sophisticated software and sleek interfaces lies a system built on the same logical principles that can be demonstrated with a carefully arranged set of dominoes.