How Binary Addition Works in Computer Architecture: From Bits to Blazing Speed

At the heart of every modern computer lies a fundamental process: binary addition. While we marvel at the complex calculations our devices perform in milliseconds, it's worth understanding that all these operations - from rendering graphics to running AI algorithms - ultimately break down into sequences of simple mathematical operations at the binary level.

The Foundation of Computer Arithmetic: Binary Addition

Computers are constantly performing basic arithmetic operations - adding, multiplying, comparing, and moving numbers. For these operations to be practical in solving complex problems, they must be executed with remarkable speed and efficiency. The most fundamental of these operations is binary addition, which forms the building block for virtually all computer calculations.

Binary addition in computer architecture follows a similar principle to how we add decimal numbers. Just as we add numbers digit by digit and carry values when needed, computers add binary digits (bits) one pair at a time, managing carries along the way. The key difference is that computers work with only two digits: 0 and 1.

Full adder circuits arranged to process binary digits, showing how computers break down complex calculations into simple binary addition operations

The Full Adder: Building Block of Binary Addition

At the core of binary addition in computer science is a circuit called a full adder. This ingenious component adds two bits plus a possible carry bit from a previous addition, producing both a sum bit and a potential carry bit for the next addition.

When adding 1 + 0 with no carry input: produces sum 1, no carry output
When adding 1 + 0 with a carry input of 1: produces sum 0, carry output 1
When adding 1 + 1 with no carry input: produces sum 0, carry output 1
When adding 1 + 1 with a carry input of 1: produces sum 1, carry output 1

While these operations seem simple, they're the foundation upon which all computer arithmetic is built. By combining full adders, we can create circuits capable of adding numbers of any size.

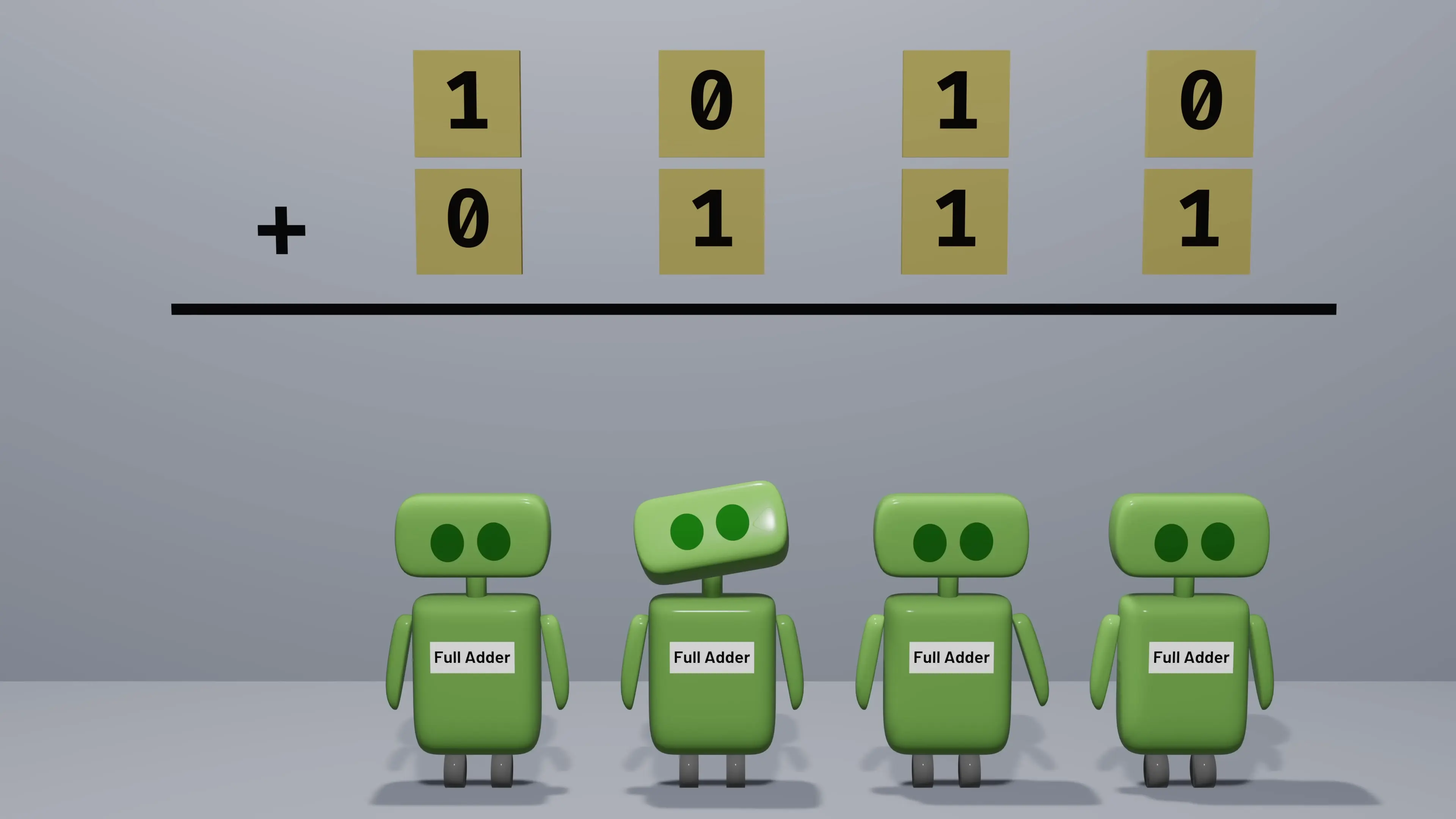
The Ripple Carry Adder: Chaining Full Adders Together

To add multi-bit numbers, computers can chain full adders together in what's called a ripple carry adder. For example, to add two 4-bit numbers, four full adders would be connected sequentially. The first adder processes the rightmost (least significant) bits and passes its carry to the next adder, which then computes its sum and passes its carry forward, and so on.

This approach works, but it has a significant limitation in computer architecture: as the numbers get larger, the addition takes longer because each adder must wait for the carry bit from the previous adder before it can complete its calculation. This creates a ripple effect that slows down the entire operation.

Full adders with propagate functions demonstrating how binary addition works in computer systems, showing the flow of carry bits between adders

The Carry Look-Ahead Adder: Revolutionizing Binary Addition Speed

To overcome the speed limitations of ripple carry adders, computer architects developed the carry look-ahead adder. This ingenious design dramatically accelerates binary addition by calculating all carry bits simultaneously rather than waiting for them to propagate through the chain.

The carry look-ahead adder introduces two important concepts in binary addition:

Generate: When an addition will produce a carry regardless of whether there's an input carry (occurs when both input bits are 1)
Propagate: When an addition will pass along a carry if one comes in (occurs when at least one input bit is 1)

By determining whether each bit position will generate or propagate a carry, the circuit can calculate all carry bits in parallel using logical formulas rather than waiting for sequential processing.

TEXT

# Logical formulas for carry bits in a 4-bit carry look-ahead adder

C1 = G0                          # Carry from bit position 0 is just its generate value
C2 = G1 + (P1 · G0)              # Carry from bit position 1
C3 = G2 + (P2 · G1) + (P2 · P1 · G0)  # Carry from bit position 2
C4 = G3 + (P3 · G2) + (P3 · P2 · G1) + (P3 · P2 · P1 · G0)  # Carry from bit position 3

Where:
Gi = Ai · Bi          # Generate at position i (both bits are 1)
Pi = Ai + Bi          # Propagate at position i (at least one bit is 1)

These formulas may look complex, but they can be computed very quickly in hardware - typically in just two logical steps regardless of the number of bits being added. This is what makes carry look-ahead logic so powerful for binary addition in computer architecture.

Binary addition process visualized with number cards and full adder components, illustrating the fundamental mathematical operations that power computer calculations

Hierarchical Carry Look-Ahead: Scaling for Larger Numbers

As the number of bits increases, the carry look-ahead formulas become unwieldy with too many terms. To address this, computer architects implement hierarchical carry look-ahead systems. These systems group bits together (commonly in 4-bit blocks) and apply carry look-ahead logic at multiple levels.

Each 4-bit block calculates its own generate and propagate values, and a higher-level carry look-ahead unit uses these block-level values to determine the carry inputs for each block. This hierarchical approach maintains the speed advantage while scaling to handle larger numbers efficiently.

Why Binary Addition Speed Matters in Computer Systems

The speed of binary addition might seem like a minor concern when measured in nanoseconds, but it becomes critical when you consider that computers perform billions of operations per second. Those nanoseconds add up quickly, especially in applications requiring intensive calculations like scientific simulations, graphics rendering, or machine learning.

By implementing carry look-ahead logic, computer architects have enabled our devices to perform binary addition with remarkable efficiency. This optimization stands as a perfect example of how understanding the fundamental operations of computing can lead to dramatic performance improvements at scale.

Practical Applications of Binary Addition in Modern Computing

Fast binary addition is primarily used for numerous essential operations in computer systems:

Arithmetic Logic Units (ALUs) in CPUs rely on binary addition for most calculations
Floating-point operations for scientific and graphical applications
Memory address calculations for accessing data
Digital signal processing for audio, video, and communications
Cryptographic algorithms for security applications

Even operations that don't seem like addition at first glance - such as multiplication, which can be implemented as repeated addition, and subtraction, which uses two's complement representation - ultimately rely on the same binary addition circuits.

Conclusion: The Power of Parallelism in Computer Architecture

The evolution from ripple carry adders to carry look-ahead adders demonstrates a fundamental principle in computer architecture: parallelism leads to speed. By identifying tasks that can be performed simultaneously rather than sequentially, computer designers have dramatically accelerated binary addition and, by extension, virtually all computer operations.

Understanding binary addition in computer architecture provides insight into how our modern digital world functions at its most fundamental level. From the simplest calculator to the most powerful supercomputer, the ability to quickly add binary numbers remains at the core of computing - a testament to how mastering the basics can lead to extraordinary capabilities when scaled up.

How Binary Addition Works in Computer Architecture: From Simple Bits to Blazing Processing Speed