How Computers Store Floating-Point Numbers: Understanding Binary Representation and IEEE Standards

Understanding how computers represent decimal values internally is crucial for programmers who need to work with precise calculations. While computers fundamentally operate using binary (zeros and ones), they need sophisticated methods to represent fractional numbers that we commonly use in the decimal system. This article explores how floating-point representation works in binary and the standards that govern it.

The Challenge of Representing Real Numbers in Binary

Computers represent all data in binary, which means every number must be stored as a sequence of zeros and ones. For non-negative integers, this is straightforward - each bit represents a power of two (1, 2, 4, 8, 16, etc.), and we simply add up the place values for each bit that has a value of 1.

However, representing numbers with fractional parts presents a challenge. There are infinitely many real numbers, but we only have a finite number of bits to represent them. This fundamental limitation means that some numbers cannot be represented exactly in binary, leading to approximation errors.

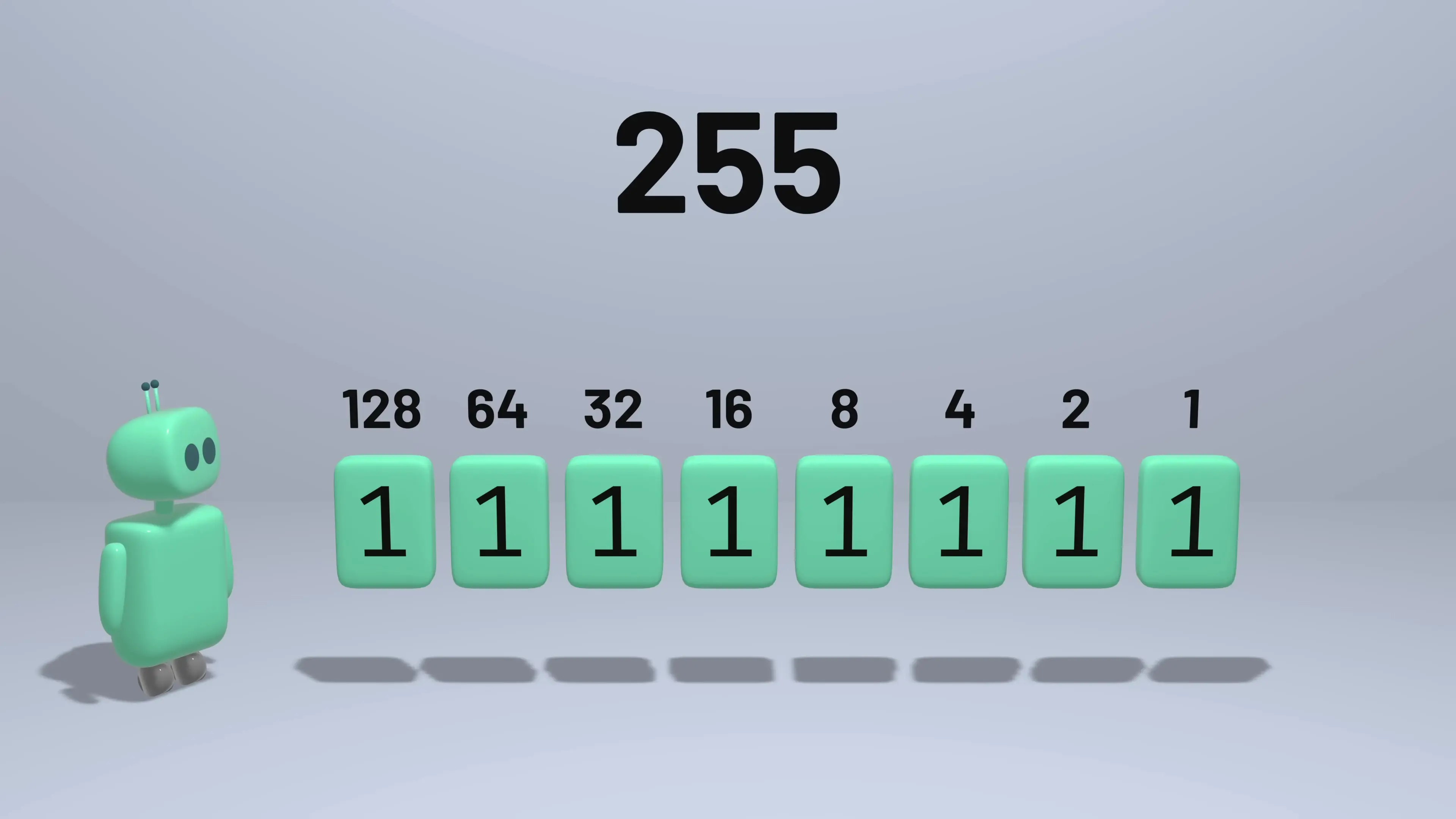
Fixed-Point vs. Floating-Point Representation

There are two primary approaches to representing numbers with fractional parts in binary:

Fixed-Point Representation

In fixed-point representation, we allocate a fixed number of bits for the integer part and a fixed number of bits for the fractional part. For example, we might use 4 bits for the integer portion (representing 1, 2, 4, and 8) and 4 bits for the fractional portion (representing 1/2, 1/4, 1/8, and 1/16).

With this approach, some numbers like 1.0, 2.0, or 4.75 can be represented precisely. However, many numbers like 2.8 cannot be represented exactly because there's no combination of the available fractions that equals 2.8 exactly.

Floating-Point Representation

The floating-point representation is similar to scientific notation in the decimal system. Instead of having separate integer and fractional parts, a floating-point number consists of a mantissa (also called significand) and an exponent.

In decimal scientific notation, we might write 128 as 1.28 × 10². Similarly, 0.0042 could be written as 4.2 × 10⁻³. In binary floating-point representation, we use powers of 2 instead of powers of 10.

The mantissa is typically normalized to be at least 1 but less than 2, and then multiplied by 2 raised to the exponent. This approach allows us to represent a much wider range of numbers with the same number of bits, although with varying precision.

The IEEE 754 Standard for Floating-Point Representation

Modern computers follow the IEEE 754 standard for representing floating-point numbers. This standard defines several formats, with the most common being single precision (32 bits) and double precision (64 bits).

Single Precision (32-bit) Format

A 32-bit floating point binary representation consists of:

• 1 bit for the sign (0 for positive, 1 for negative)
• 8 bits for the exponent
• 23 bits for the mantissa

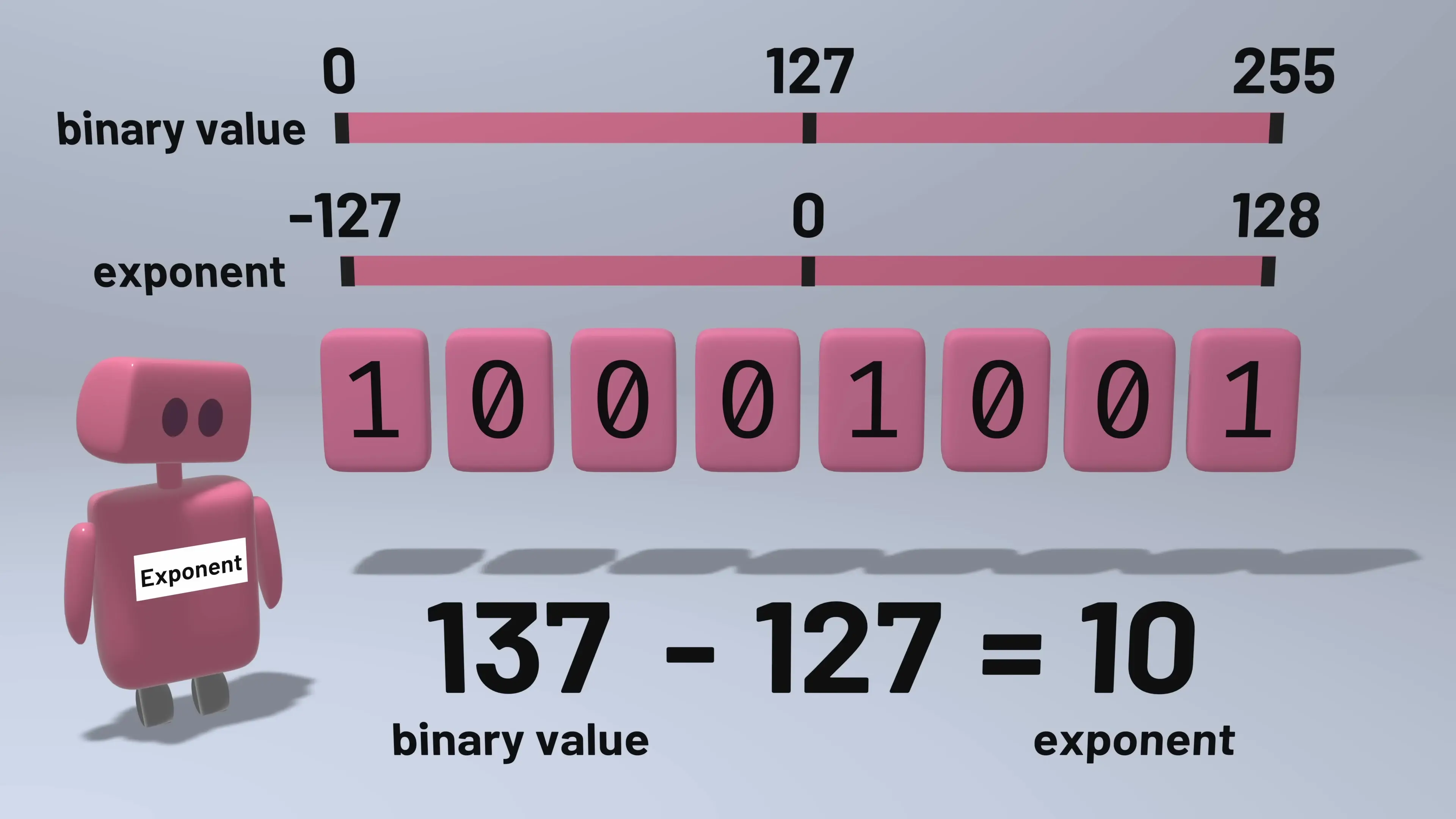
The exponent field uses a "biased representation" to handle both positive and negative exponents. With 8 bits, we can represent values from 0 to 255. To allow for negative exponents, we subtract 127 from the stored value. So a stored exponent of 127 represents an actual exponent of 0, values above 127 represent positive exponents, and values below 127 represent negative exponents.

For the mantissa, an interesting optimization is used. Since all normalized numbers have a mantissa between 1 and 2, the leading 1 is implicit and not stored. This gives us an effective 24 bits of precision for the mantissa despite only storing 23 bits.

Double Precision (64-bit) Format

The double precision floating point binary representation follows the same principle but with more bits:

• 1 bit for the sign
• 11 bits for the exponent
• 52 bits for the mantissa

This allows for a much wider range of values and greater precision than single precision.

Special Cases in Floating-Point Representation

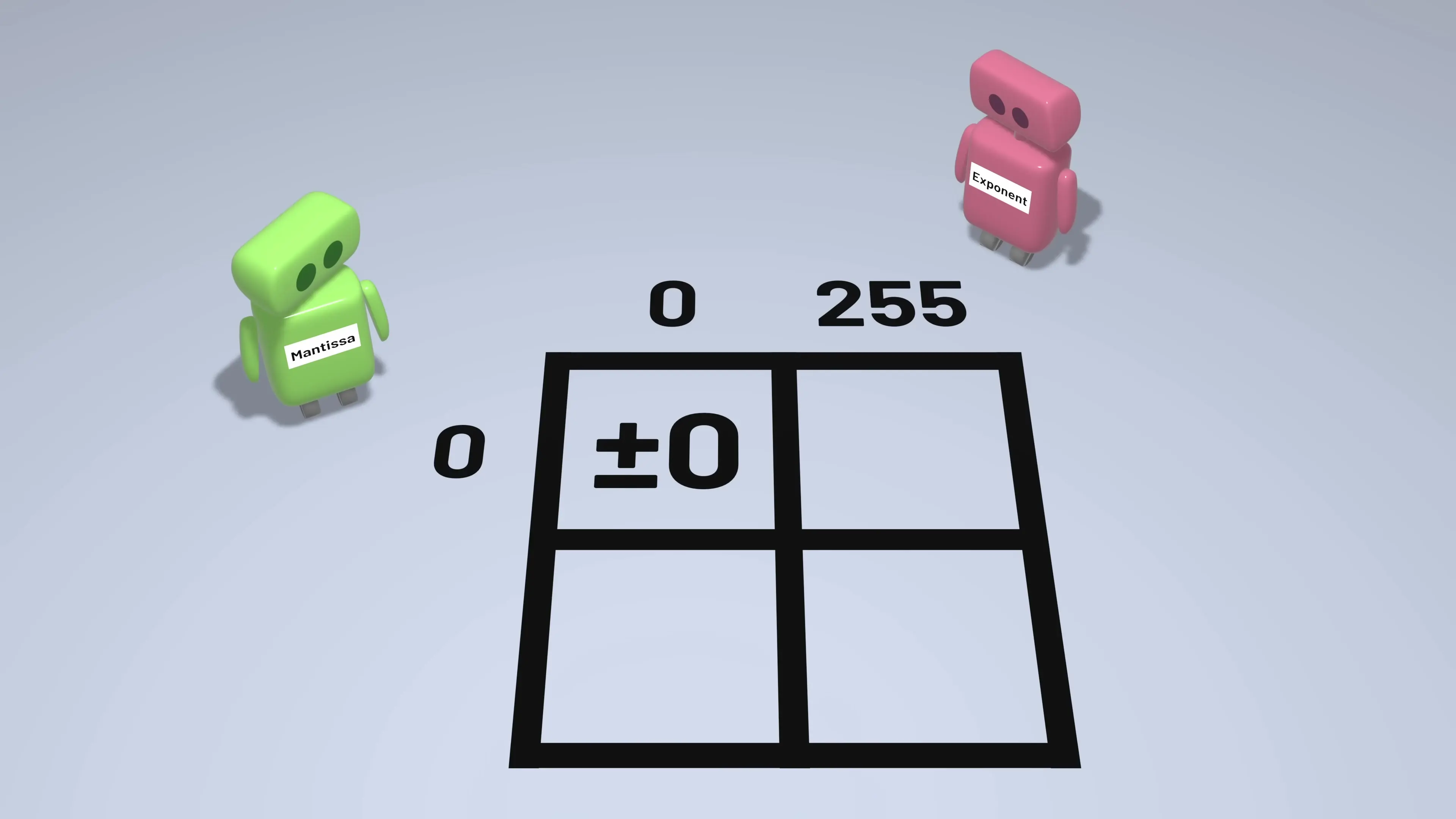
The IEEE standard includes special cases to represent values that don't fit the normal pattern:

• Zero: Represented by an exponent of 0 and a mantissa of 0
• Infinity: Represented by an exponent of 255 (for single precision) and a mantissa of 0
• NaN (Not a Number): Represented by an exponent of 255 and a non-zero mantissa
• Subnormal numbers: Used for very small numbers near zero, represented by an exponent of 0 and a non-zero mantissa

Interpreting a Floating-Point Number

To interpret a normal floating-point number:

1. Extract the sign bit to determine if the number is positive or negative
2. Extract the exponent and subtract the bias (127 for single precision, 1023 for double precision)
3. Extract the mantissa and add the implicit leading 1
4. Calculate the final value: (-1)^sign × mantissa × 2^exponent

Precision Limitations in Floating-Point Representation

While floating-point representation allows computers to work with a wide range of numbers, it comes with limitations. The most significant is that many decimal numbers cannot be represented exactly in binary floating-point format.

For example, the decimal value 0.1 cannot be represented exactly in binary floating-point. This leads to small rounding errors that can accumulate in calculations, potentially causing significant discrepancies in programs that require high precision.

Additionally, the precision of floating-point numbers varies across their range. Very large and very small numbers have less precision than numbers closer to 1. This is a trade-off made to allow for the wide dynamic range that floating-point representation provides.

Practical Implications for Developers

Understanding floating-point representation is crucial for developers who work with numerical computations. Here are some practical implications:

• Never test floating-point numbers for exact equality; instead, check if they're close enough within some tolerance
• Be aware that calculations involving very large and very small numbers together may lose precision
• Consider using decimal types or fixed-point arithmetic for financial calculations where exact decimal representation is required
• Understand that repeated calculations can accumulate rounding errors

Conclusion

Floating-point representation is a sophisticated solution to the challenge of representing real numbers in binary. The IEEE 754 standard provides a consistent approach across different computer systems, allowing for both a wide range of values and reasonable precision for most applications.

While it has limitations, understanding these limitations is key to writing robust numerical software. By knowing how floating-point numbers are represented and the potential pitfalls, developers can make informed decisions about when to use floating-point arithmetic and when alternative approaches might be more appropriate.