Understanding Logic Gates: The Fundamental Building Blocks of Computer Circuits Explained

Inside your computer are billions of tiny transistors that function essentially as microscopic switches. These switches can be either on (represented by 1) or off (represented by 0), forming the binary number system that serves as the fundamental language of computing. But how do these simple binary states transform into the complex operations that power our digital world? The answer lies in logic gates - the foundational building blocks of computer circuits.

What Are Logic Gates?

Logic gates are the elementary building blocks of digital circuits. They perform basic logical functions by taking one or more binary inputs and producing a single binary output based on specific logical rules. These gates process the binary information stored in computers, transforming inputs into outputs according to predefined logical operations.

Basic Logic Gates and Their Truth Tables

Let's explore the fundamental logic gates that form the basis of all computer operations. For each gate, we'll examine its function and corresponding truth table - a tabular representation that defines the output for every possible input combination.

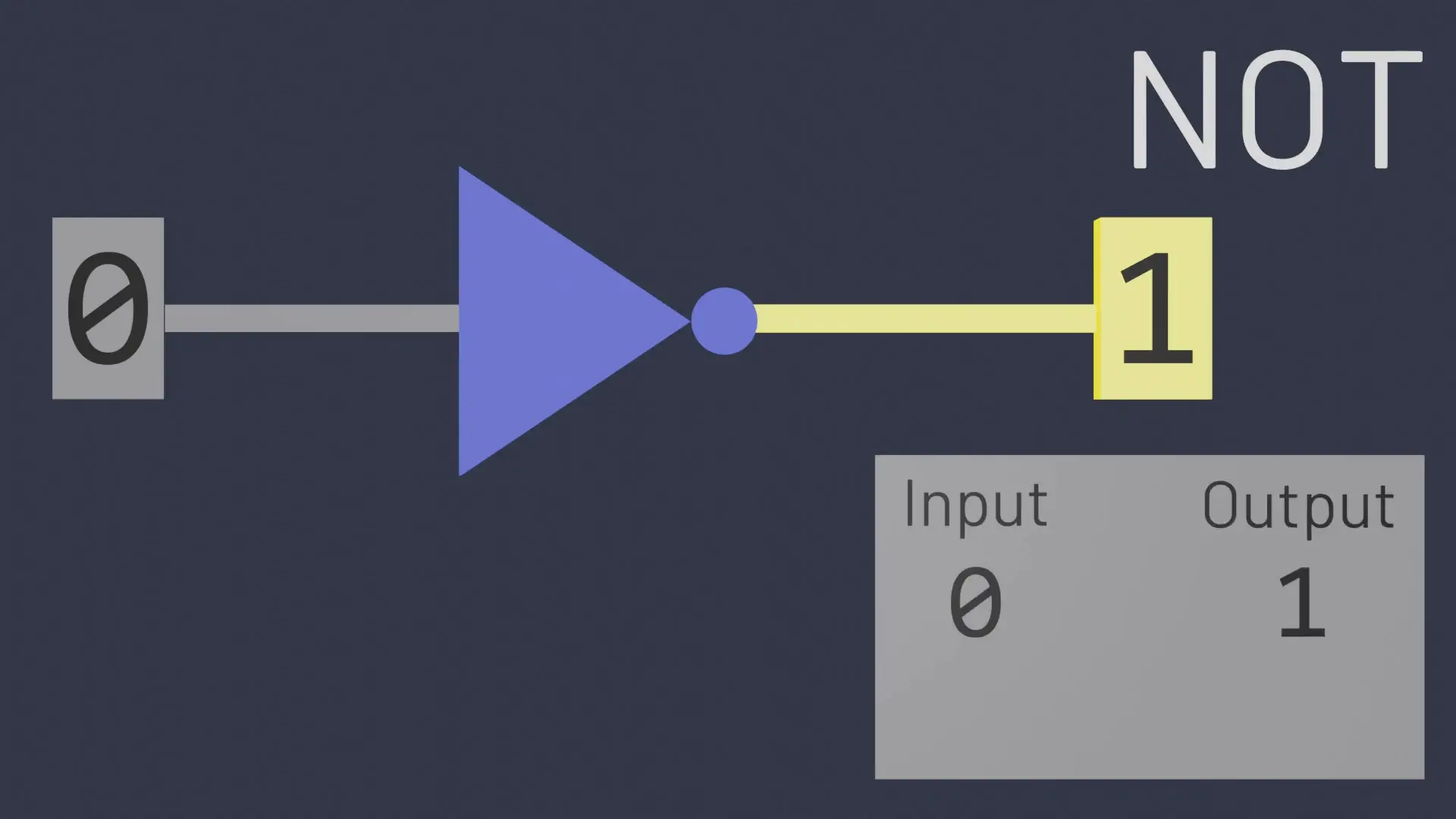
The NOT Gate (Inverter)

The NOT gate is one of the simplest logic gates. It takes a single input and inverts it, producing the opposite value as output. If the input is 1, the output is 0; if the input is 0, the output is 1. This operation is also called a logical negation or inversion.

The AND Gate

The AND gate accepts two inputs (A and B) and outputs 1 only when both inputs are 1. In all other cases, it outputs 0. This mimics the logical "and" operation - both conditions must be true for the result to be true.

• When A=0 and B=0, output is 0
• When A=0 and B=1, output is 0
• When A=1 and B=0, output is 0
• When A=1 and B=1, output is 1

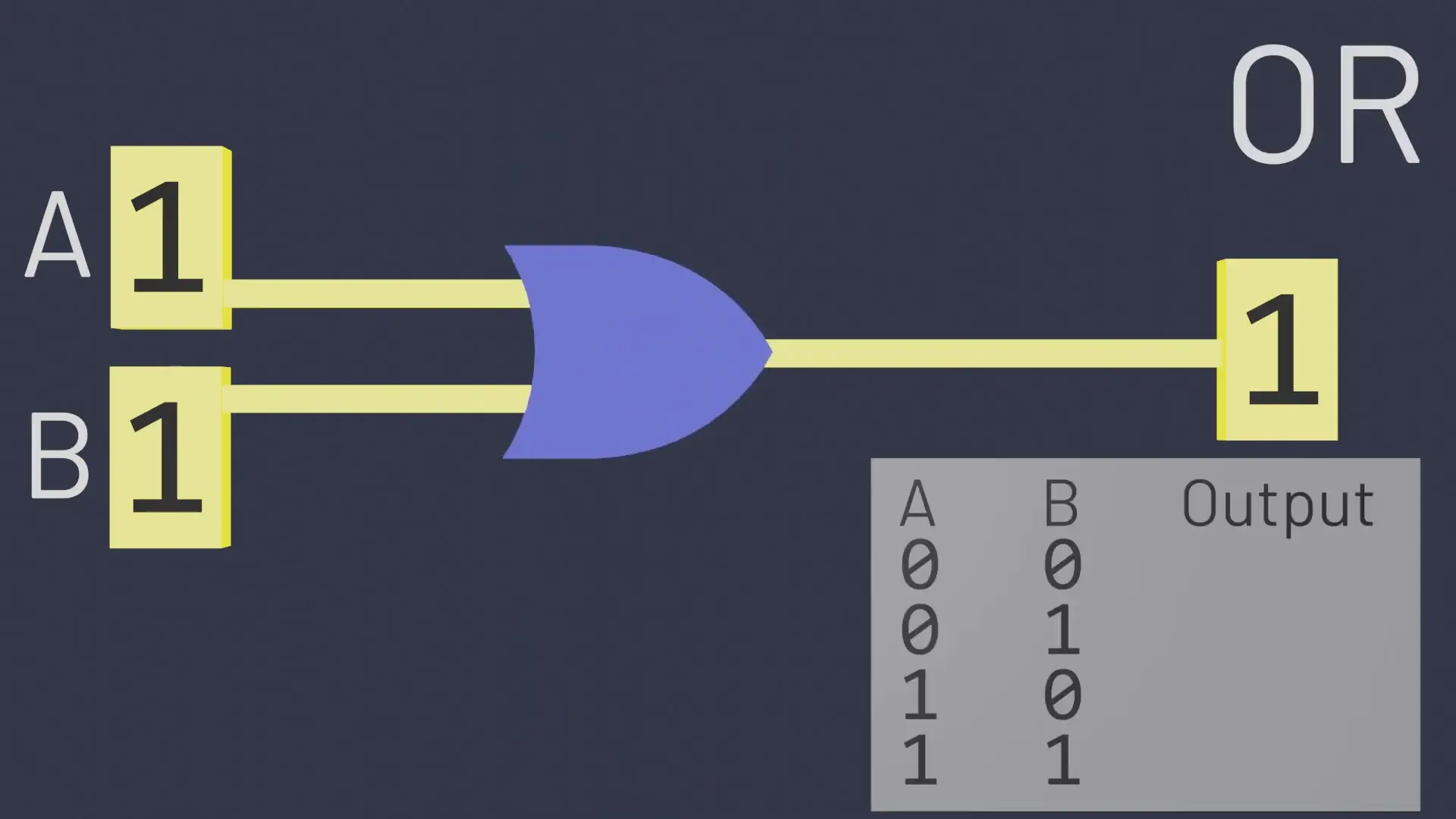
The OR Gate

The OR gate also takes two inputs but outputs 1 when either input A OR input B (or both) is 1. It outputs 0 only when both inputs are 0. This represents the logical "or" operation - at least one condition must be true for the result to be true.

• When A=0 and B=0, output is 0
• When A=0 and B=1, output is 1
• When A=1 and B=0, output is 1
• When A=1 and B=1, output is 1

Compound Logic Gates

By combining basic logic gates, we can create more complex gates that perform specialized operations. These compound gates are essential for building sophisticated digital circuits.

The NAND Gate

The NAND gate is essentially an AND gate followed by a NOT gate. It performs the opposite function of an AND gate, outputting 0 only when both inputs are 1, and outputting 1 in all other cases. NAND is particularly important in computing because it's considered a universal gate - any logical function can be implemented using only NAND gates.

The NOR Gate

Similar to NAND, the NOR gate is an OR gate followed by a NOT gate. It outputs 1 only when both inputs are 0, and outputs 0 in all other cases. Like NAND, NOR is also a universal gate, meaning any logical function can be constructed using only NOR gates.

The XOR Gate (Exclusive OR)

The XOR (Exclusive OR) gate outputs 1 when exactly one of its inputs is 1. If both inputs are the same (both 0 or both 1), it outputs 0. This gate is particularly useful for binary addition and comparison operations.

• When A=0 and B=0, output is 0
• When A=0 and B=1, output is 1
• When A=1 and B=0, output is 1
• When A=1 and B=1, output is 0

The XNOR Gate (Exclusive NOR)

The XNOR gate performs the opposite function of XOR. It outputs 1 when both inputs are the same (both 0 or both 1) and outputs 0 when the inputs are different. This gate is useful for equivalence checking and is sometimes called an equality comparator.

How to Learn Logic Gates Easily

Understanding logic gates can seem challenging at first, but there are several approaches that can make learning them much easier:

1. Start with truth tables: Memorizing the truth tables for each gate provides a solid foundation for understanding their behavior.
2. Use visual representations: Diagrams and circuit symbols help visualize how gates process information.
3. Practice with examples: Work through simple problems to reinforce your understanding of how gates process different input combinations.
4. Build from simple to complex: Master the basic gates (NOT, AND, OR) before moving on to compound gates.
5. Relate to everyday logic: Connect gate operations to everyday logical thinking ("both conditions must be true" for AND, "at least one condition must be true" for OR).

Practical Applications of Logic Gates

Logic gates aren't just theoretical constructs - they have numerous practical applications in computing and electronics:

• Arithmetic operations: Logic gates form the basis for binary addition, subtraction, multiplication, and division circuits.
• Memory storage: Flip-flops and latches built from logic gates store binary information in computer memory.
• Decision making: Computers use logic gates to evaluate conditions and make decisions based on programmed logic.
• Data processing: From simple data validation to complex calculations, logic gates process information in CPUs.
• Signal processing: Logic gates help filter, amplify, and transform electronic signals in various devices.
• Control systems: Everything from traffic lights to industrial automation relies on logic gates for control logic.

From Simple Gates to Complex Computers

The remarkable aspect of logic gates is how these simple components combine to create increasingly complex systems. By connecting multiple gates together, engineers build circuits that can perform sophisticated operations like addition, subtraction, comparison, and data storage. These circuits then combine to form larger functional units like arithmetic logic units (ALUs), memory modules, and ultimately complete computer processors.

This hierarchical design - building complex systems from simple components - is what enables modern computers to perform their seemingly magical functions while ultimately operating on nothing more than billions of binary switches. From displaying images and playing videos to browsing the web and running complex applications, all computer operations can be broken down into combinations of these fundamental logic operations.

Conclusion

Logic gates form the fundamental building blocks of all digital computing. By understanding these basic components and how they combine to form more complex systems, we gain insight into how computers transform simple binary information into the sophisticated operations that power our digital world. Whether you're studying computer science, working with digital electronics, or simply curious about how computers work, a solid understanding of logic gates provides an essential foundation for exploring the fascinating world of digital technology.