Understanding Propositional Logic: The Mathematical Foundation of Computer Reasoning

Logic is the foundation upon which all computer operations are built. From the ringtone that plays when you receive a call (but only if your phone isn't on silent mode) to the login button that activates only when both username and password fields are correctly filled, logical reasoning dictates how computers make decisions based on whether statements are true or false.

What is Propositional Logic?

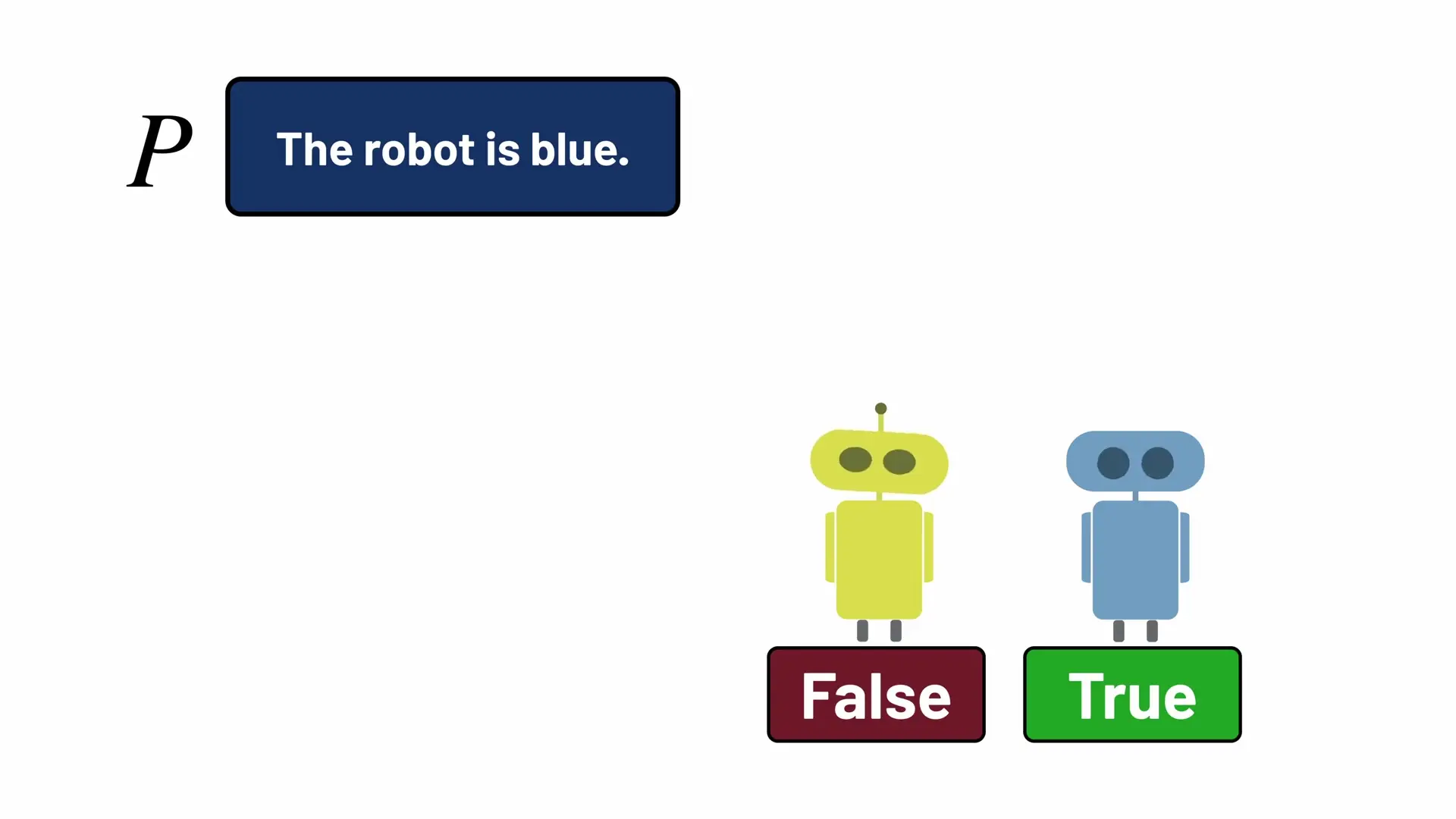
Propositional logic (also known as propositional calculus) is one of the most fundamental logical systems used in computer science. It deals with propositions—statements that can be either true or false, but not both simultaneously. For instance, "The robot is blue" is a proposition that could be either true or false depending on the actual color of the robot.

To simplify discussions about these propositions, we use variables (like P or Q) to represent them. This abstraction allows us to focus on the logical relationships rather than the specific content of each statement.

Logical Operators in Propositional Logic

The power of propositional logic comes from our ability to modify and combine logical variables into more complex formulas using logical operators. These operators are the building blocks for creating sophisticated logical expressions that computers can evaluate.

Negation (NOT)

The negation operator (¬) reverses the truth value of a proposition. If P represents "The robot is blue," then ¬P (not P) means "The robot is not blue." When P is true, ¬P is false, and vice versa.

Conjunction (AND)

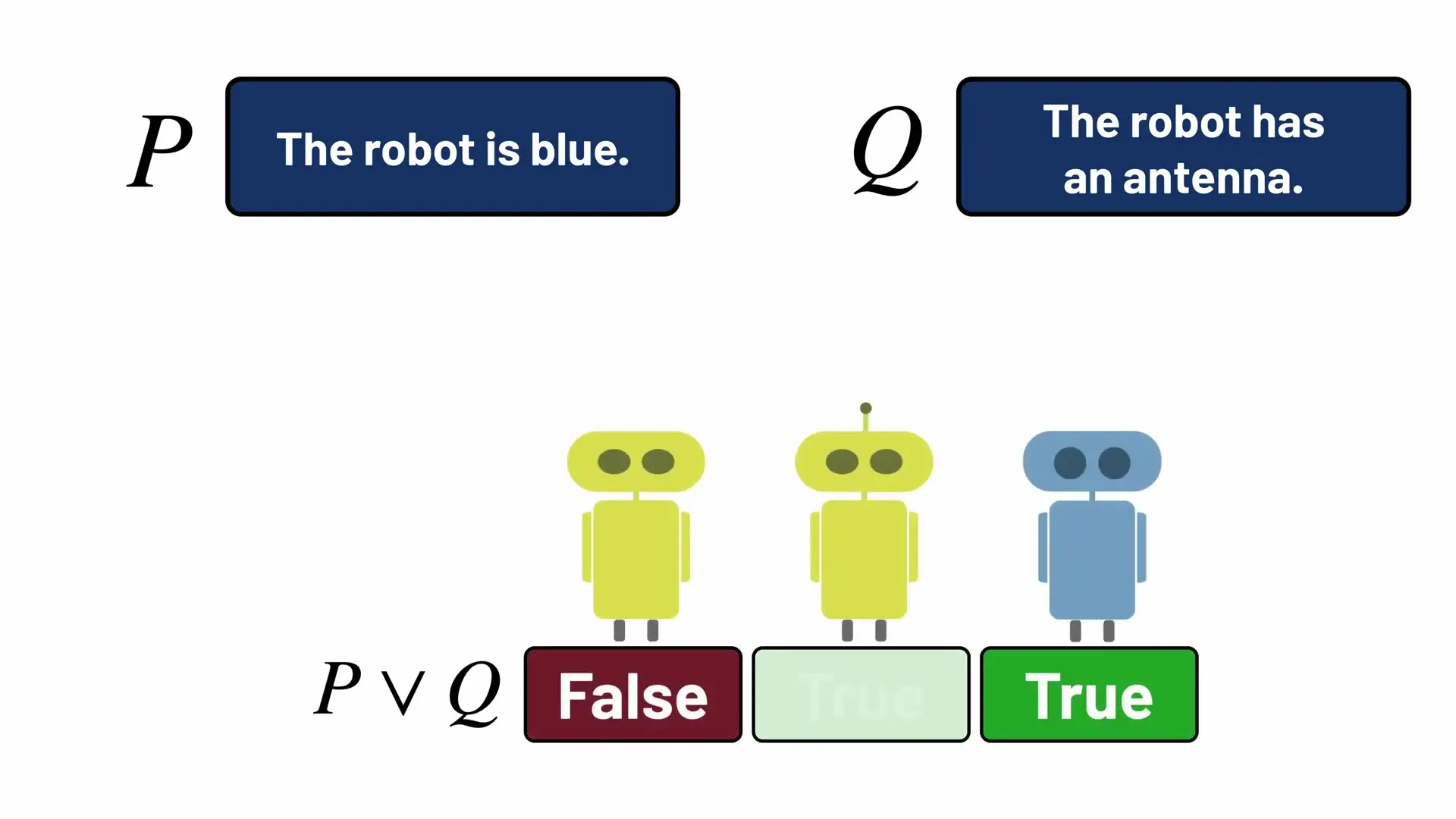
The conjunction operator (∧) combines two propositions and is true only when both propositions are true. If P means "The robot is blue" and Q means "The robot has an antenna," then P ∧ Q is true only when the robot is both blue and has an antenna.

Disjunction (OR)

The disjunction operator (∨) is true when at least one of the propositions is true. Using our robot example, P ∨ Q is true if the robot is blue, has an antenna, or both. It's only false when both P and Q are false.

Exclusive OR (XOR)

The exclusive OR operator (⊕) is true when exactly one of its operands is true, but not both. P ⊕ Q is true when either the robot is blue or it has an antenna, but not when both conditions are true or both are false.

Implication (→)

The implication operator (→) represents a conditional relationship between propositions. P → Q (read as "P implies Q" or "if P then Q") is false only when P is true and Q is false. In all other cases, it's true. This means that if the robot is blue (P is true), then it must have an antenna (Q must be true) for P → Q to be true.

An important characteristic of implication is that it's always true when the antecedent (P) is false, regardless of whether the consequent (Q) is true or false. This aligns with how we use "if-then" statements in everyday language.

Biconditional (↔)

The biconditional operator (↔) represents "if and only if" and is true when both propositions have the same truth value—either both are true or both are false. P ↔ Q means that P implies Q and Q implies P.

Truth Tables: Visualizing Logical Relationships

When dealing with multiple logical variables, truth tables provide a systematic way to determine when a formula is true or false. A truth table lists all possible combinations of truth values for the variables in a formula and shows the resulting truth value of the entire formula.

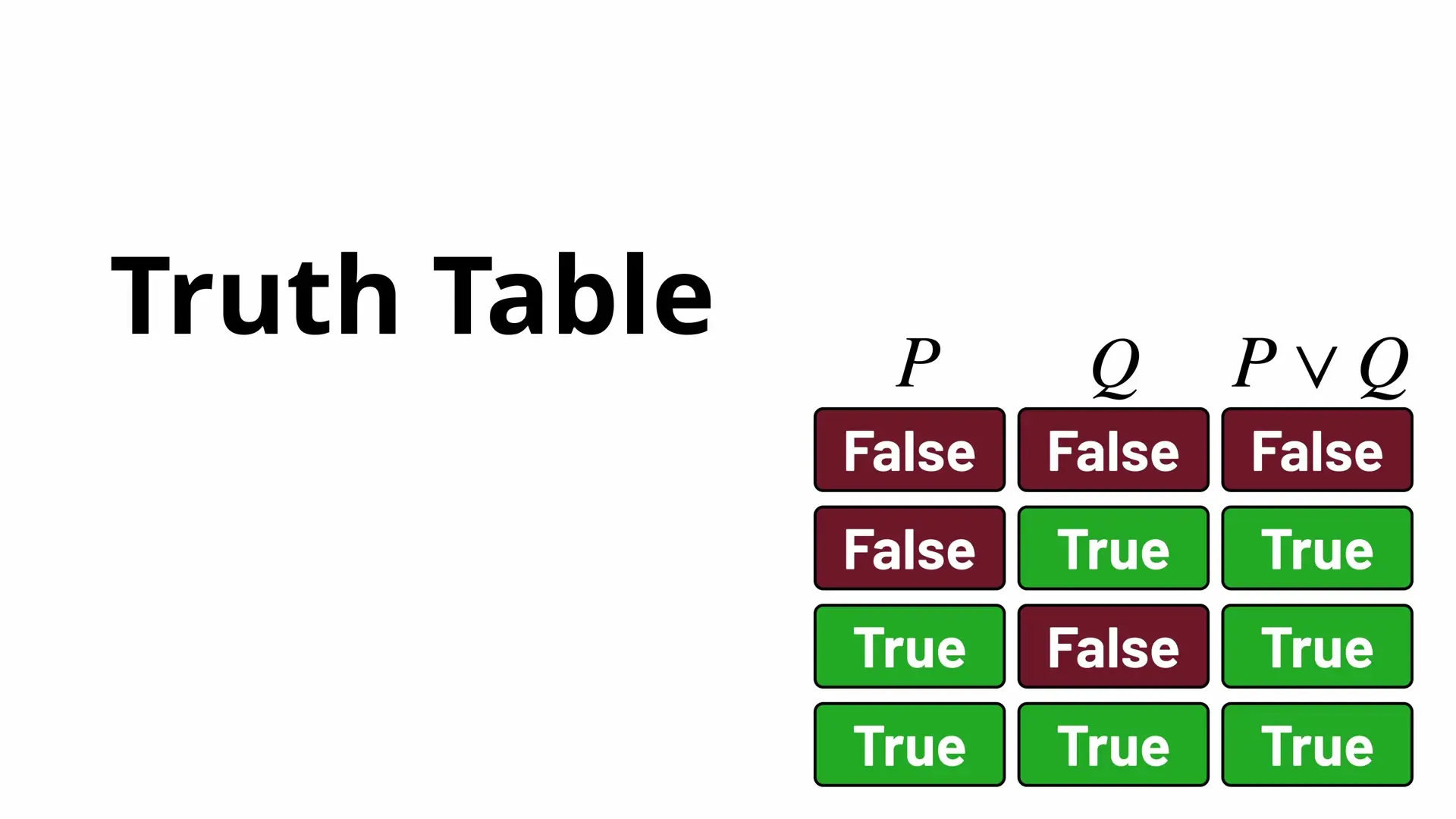
For two variables P and Q, there are four possible combinations of truth values:

• P is false, Q is false
• P is false, Q is true
• P is true, Q is false
• P is true, Q is true

For example, in the truth table for P ∧ Q (conjunction), the formula is true only when both P and Q are true. In all other cases, it's false. Conversely, for P ∨ Q (disjunction), the formula is true in three out of four cases, being false only when both P and Q are false.

Logical Equivalence and Proofs

Two logical formulas are equivalent if they have identical truth tables—that is, they yield the same truth value for all possible combinations of their variables. For instance, P → Q is logically equivalent to ¬P ∨ Q, which can be proven by comparing their truth tables.

Understanding logical equivalences is crucial for simplifying complex logical expressions and for constructing logical proofs (preuve simple logique). For example, we can prove that P ⊕ Q is equivalent to (P ∧ ¬Q) ∨ (¬P ∧ Q) by comparing their truth tables.

Proving Non-Equivalence

Not all seemingly similar formulas are equivalent. For example, P → Q is not equivalent to Q → P. We can demonstrate this through truth tables: when P is true and Q is false, P → Q is false, but Q → P is true. This makes intuitive sense; "if it's a holiday, then the bank is closed" doesn't mean the same thing as "if the bank is closed, then it's a holiday."

Applications in Computer Science

Propositional logic forms the foundation for many aspects of computer science and programming:

• Boolean logic in programming languages (if-then-else statements, logical operators)
• Circuit design and digital electronics
• Database queries and search algorithms
• Artificial intelligence and expert systems
• Formal verification of software and hardware systems
• Predicate logic resolution for automated theorem proving

Real-Life Examples of Propositional Logic

Propositional logic is embedded in countless everyday technologies:

1. Smartphone notifications ("If it's a message AND not in silent mode, then play sound")
2. Authentication systems ("If username is correct AND password is correct, then grant access")
3. Smart home devices ("If motion is detected AND it's after sunset, then turn on lights")
4. Search filters ("Show results that contain keyword1 OR keyword2 BUT NOT keyword3")
5. Form validation ("If all required fields are filled AND the email format is valid, then enable submit button")

Building Propositional Logic Trees

Propositional logic trees (also called syntax trees or parse trees) provide a visual representation of how complex logical formulas are constructed from simpler components. They help in understanding the structure and evaluation order of logical expressions.

For example, the formula (P ∧ Q) → (¬P ∨ R) can be represented as a tree with the main implication operator at the root, the conjunction P ∧ Q as the left subtree, and the disjunction ¬P ∨ R as the right subtree.

Conclusion: The Power of Formal Logic

Propositional logic provides a formal language for expressing logical relationships with precision and clarity. By learning this language, we gain the ability to communicate with computers on their terms, using the same building blocks that underlie all computational reasoning.

While the symbols and formulas may seem abstract at first, they capture intuitive ideas about how we reason in everyday life. The difference is that propositional logic formalizes these ideas with mathematical precision, making them suitable for implementation in computers.

As we continue to build increasingly sophisticated technology, understanding the fundamentals of propositional logic becomes ever more valuable—not just for computer scientists and programmers, but for anyone who wants to understand how the digital world around us works.