Understanding B-Trees: How Modern Databases Store and Retrieve Data Efficiently

When designing systems that need to store and operate on large amounts of data, choosing the right data structure is crucial for performance. While many developers are familiar with binary search trees, the B-tree data structure is what powers most modern database systems, offering superior efficiency for disk-based storage. This comprehensive guide explores how B-trees work and why they're the preferred choice for database implementations.

Binary search tree structure showing hierarchical organization with numerical keys, demonstrating the foundation that evolved into the more efficient B-tree structures used in modern database systems.

Binary Search Trees: The Foundation

Before diving into B-trees, it's important to understand binary search trees (BSTs). A binary search tree consists of nodes, each containing a key (typically a unique number) and pointers to at most two child nodes—a left child and a right child.

Binary search trees follow a simple property: for any node, all keys in its left subtree are less than the node's key, and all keys in its right subtree are greater than the node's key. This property enables efficient search operations with a time complexity of O(log n) in balanced trees.

How Binary Search Trees Work

When searching for a key in a binary search tree, we start at the root node and compare our target key with the node's key. If they match, we've found what we're looking for. If our target key is smaller, we move to the left child; if larger, we move to the right child. This process continues until we either find the key or reach a leaf node (indicating the key doesn't exist in the tree).

The beauty of this approach is that at each step, we eliminate roughly half of the remaining search space, making the search process logarithmic rather than linear.

The Limitations of Binary Search Trees for Databases

While binary search trees are efficient for in-memory operations, they're not ideal for database systems where data primarily resides on disk. The key insight here is understanding what operations are expensive in different contexts.

In a database environment, the most time-consuming operation isn't comparing keys (which processors can do very quickly) but rather fetching a new node from disk. When data is stored on disk, each node access requires a disk I/O operation, which is orders of magnitude slower than in-memory operations.

Visual representation of data structure principles showing numbered blocks arranged in a binary search tree pattern, illustrating how data organization affects retrieval efficiency.

Enter B-Trees: Optimized for Disk-Based Operations

This is where B-trees come into play. A B-tree is a self-balancing tree data structure that maintains sorted data and allows for efficient insertions, deletions, and searches. Unlike binary search trees where each node has at most two children, B-tree nodes can have multiple keys and children.

The core idea behind a B-tree database implementation is to reduce the number of disk accesses by storing more keys in each node. While this may increase the number of key comparisons per node, it significantly reduces the total number of nodes that need to be accessed during operations—a crucial optimization for disk-based systems.

Key Properties of B-Trees

All leaf nodes are at the same level (perfect height balance)
Each node has a maximum number of keys (order of the tree)
Each non-root node must be at least half full (minimum number of keys)
The root can have as few as one key
All keys within a node are sorted in ascending order

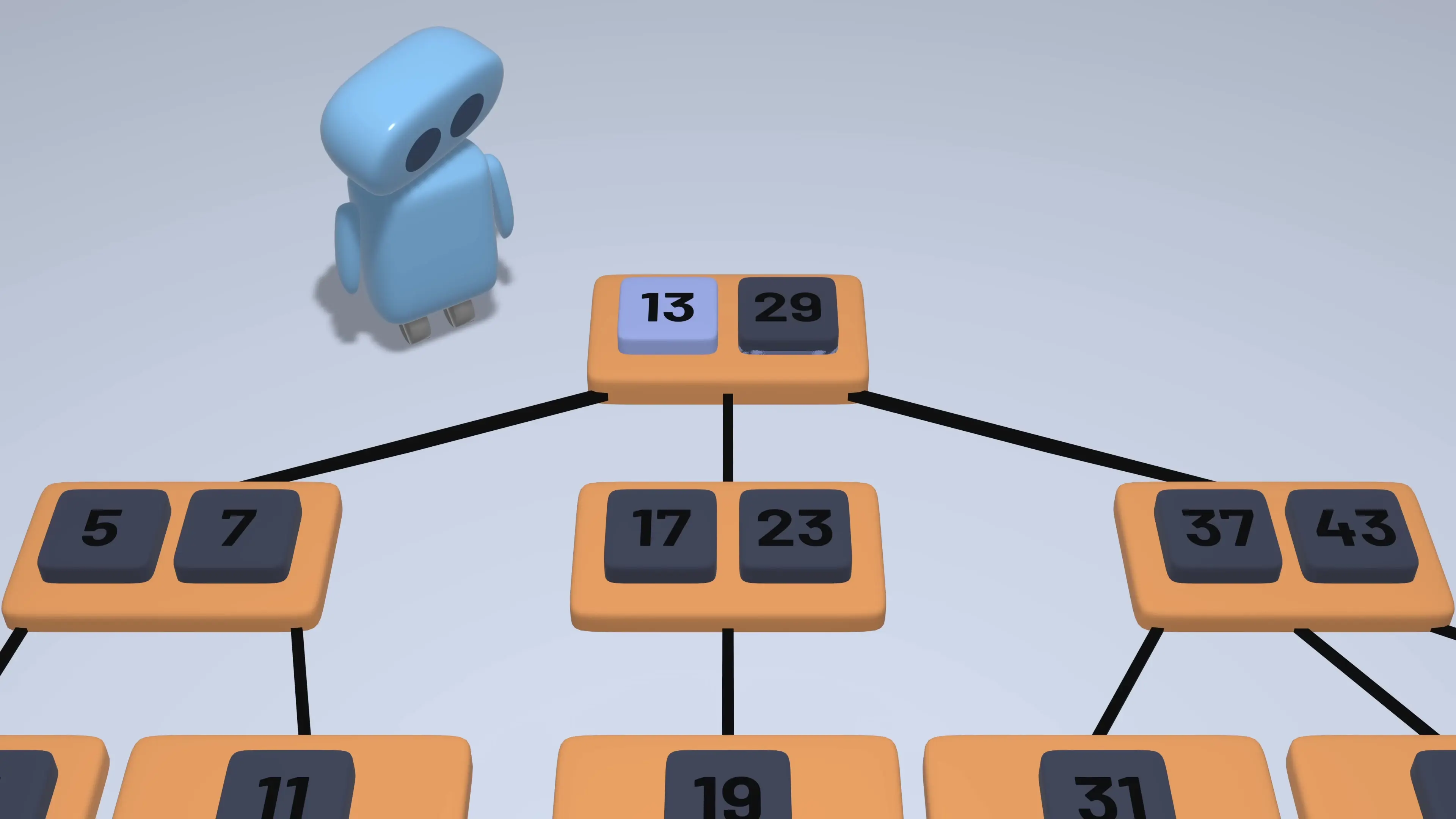
B-Tree Structure and Operations

A B-tree of order m (also called an m-way B-tree) has the following properties:

Each node can contain at most m-1 keys
Each internal node (except the root) has at least ⌈m/2⌉ children
If the root is not a leaf, it has at least 2 children
A non-leaf node with k keys has k+1 children
All leaves appear on the same level

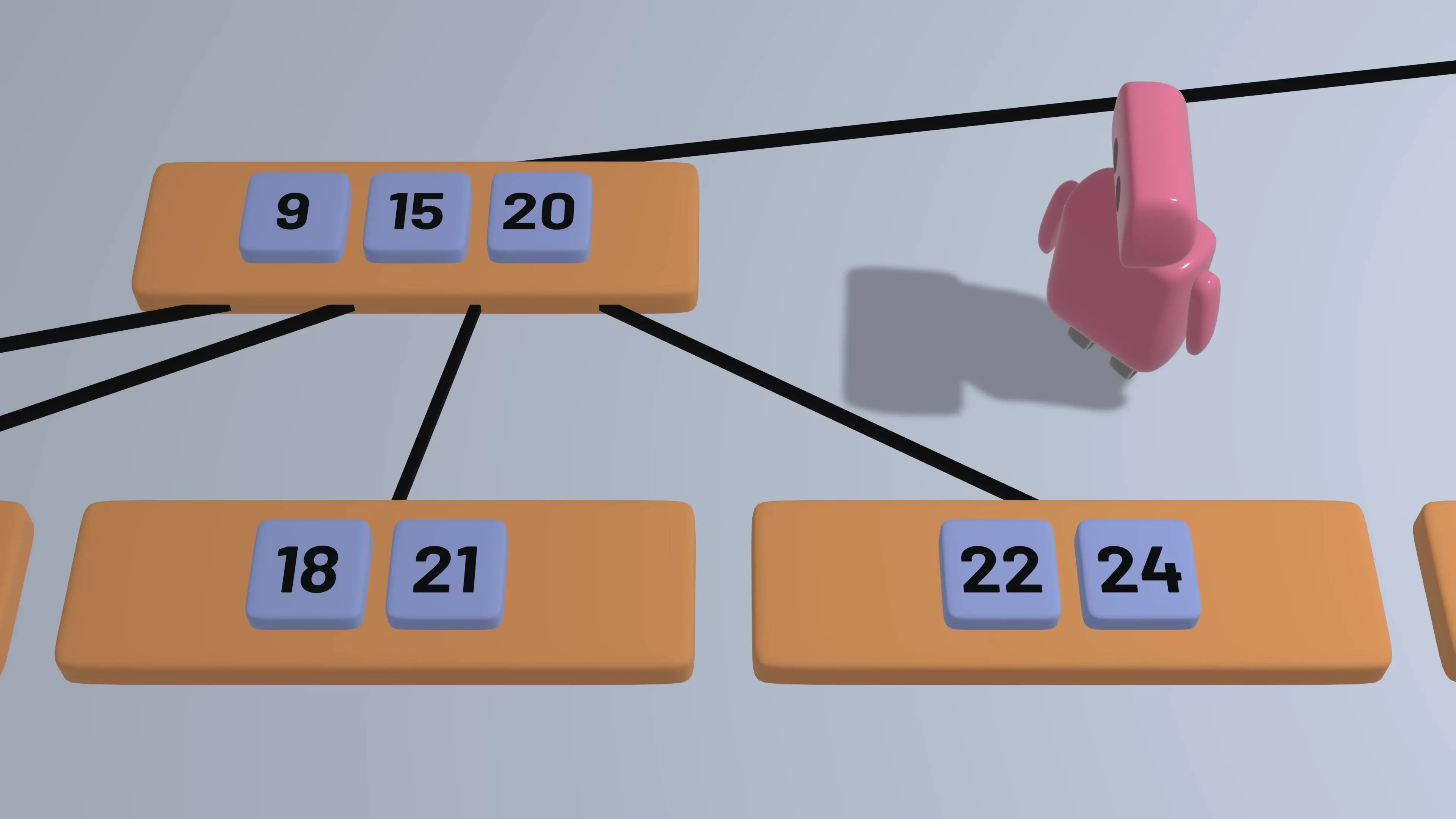
B-tree structure visualization showing multiple keys per node (9, 15, 20 at parent level and 18, 21, 22, 24 at child level), demonstrating how databases organize data to minimize disk operations.

Searching in a B-Tree

Searching in a B-tree works similarly to a binary search tree but with multiple keys per node. Starting at the root:

Compare the search key with the keys in the current node
If the key is found, the search is successful
If the key is less than the smallest key in the node, follow the leftmost child pointer
If the key is greater than the largest key in the node, follow the rightmost child pointer
Otherwise, follow the child pointer between the two keys that bound the search key
Repeat the process until either finding the key or reaching a leaf node without finding the key

Because B-trees have a higher branching factor (more children per node), they can search through large datasets with fewer node accesses than binary search trees, making them ideal for database b-tree implementations.

Insertion in a B-Tree

Inserting a key into a B-tree is more complex than in a binary search tree. The process involves:

Search for the appropriate leaf node where the key should be inserted
If the leaf node has space, insert the key in the correct sorted position
If the leaf node is full (has m-1 keys), split the node:

Find the median key
Move keys greater than the median to a new node
Push the median key up to the parent node
If the parent becomes full, recursively split it using the same process
If the root splits, create a new root with the median key, increasing the height of the tree

PYTHON

def insert_key(b_tree, key):
    # Find the appropriate leaf node
    leaf = find_leaf_node(b_tree, key)
    
    # Insert the key into the leaf
    insert_in_node(leaf, key)
    
    # If node is now overfull, split it
    if is_overfull(leaf):
        split_node(leaf)
        
    # Note: split_node would recursively handle parent splits if needed

Deletion in a B-Tree

Deletion in a B-tree maintains the property that all nodes (except possibly the root) must have at least the minimum number of keys. The process involves:

Search for the node containing the key to delete
If the key is in a leaf node, simply remove it
If the key is in an internal node, replace it with either its predecessor or successor from a leaf node
If removing a key causes a node to have fewer than the minimum required keys:

Try to redistribute keys from a sibling node that has extra keys
If redistribution isn't possible, merge the node with a sibling, pulling down a key from the parent
If the merge causes the parent to have too few keys, recursively apply the same process

Why B-Trees Excel in Database Implementations

B-trees have become the standard data structure for database index implementation for several compelling reasons:

Minimize disk I/O: By storing multiple keys per node, B-trees reduce the number of disk accesses required for operations
Self-balancing: B-trees automatically maintain balance, ensuring consistent performance regardless of the insertion order
Efficient range queries: The sorted nature of keys within nodes makes range queries efficient
Predictable performance: Operations have a guaranteed logarithmic time complexity
Space efficiency: B-trees maintain high occupancy in nodes, making efficient use of storage

B-Trees vs. B+ Trees in Database Systems

While this article focuses on B-trees, it's worth noting that many database systems actually implement a variation called B+ trees. In a B+ tree database implementation, all data records are stored in the leaf nodes, with internal nodes containing only keys for navigation. Additionally, leaf nodes are typically linked together, allowing for efficient sequential access—a common requirement in database operations.

SQL

-- Example of how B-trees power SQL indexes
CREATE TABLE customers (
    id INT PRIMARY KEY,  -- This will use a B-tree index by default
    name VARCHAR(100),
    email VARCHAR(100)
);

-- Creating a secondary B-tree index
CREATE INDEX idx_customer_email ON customers(email);

Implementing B-Trees in Real Database Systems

When implementing B-trees in a database system, several practical considerations come into play:

Node size: Typically aligned with disk block size for optimal I/O performance
Caching strategies: Frequently accessed nodes are kept in memory
Concurrency control: Mechanisms to handle multiple simultaneous operations
Recovery mechanisms: Ensuring tree integrity after system failures
Optimization for specific workloads: Read-heavy vs. write-heavy applications

Conclusion: The Enduring Importance of B-Trees

B-trees represent one of the most successful data structures in computer science, powering virtually every major database system in use today. Their elegant design specifically addresses the performance challenges of disk-based storage systems by minimizing the number of disk accesses while maintaining efficient search, insertion, and deletion operations.

Understanding B-tree database implementation is essential for database developers, system architects, and anyone working with large-scale data storage systems. As data volumes continue to grow, the principles behind B-trees remain as relevant as ever, ensuring that our database systems can efficiently handle the increasing demands of modern applications.

Understanding B-Trees: The Powerful Data Structure Behind Modern Database Performance