How Entropy-Based Token Selection Revolutionizes LLM Training

The field of large language models (LLMs) continues to evolve rapidly, with researchers constantly seeking more efficient training methods. One revolutionary approach gaining traction focuses on the concept of token entropy and its role in reinforcement learning with verifiable rewards (RLVR).

Understanding RLVR and the Token Problem

Reinforcement Learning with Verifiable Rewards (RLVR) trains models toward specific behaviors through environments that can be systematically verified, such as mathematics and coding. This approach allows for scaling up the learning process significantly, but it faces a fundamental challenge: reward assignment precision.

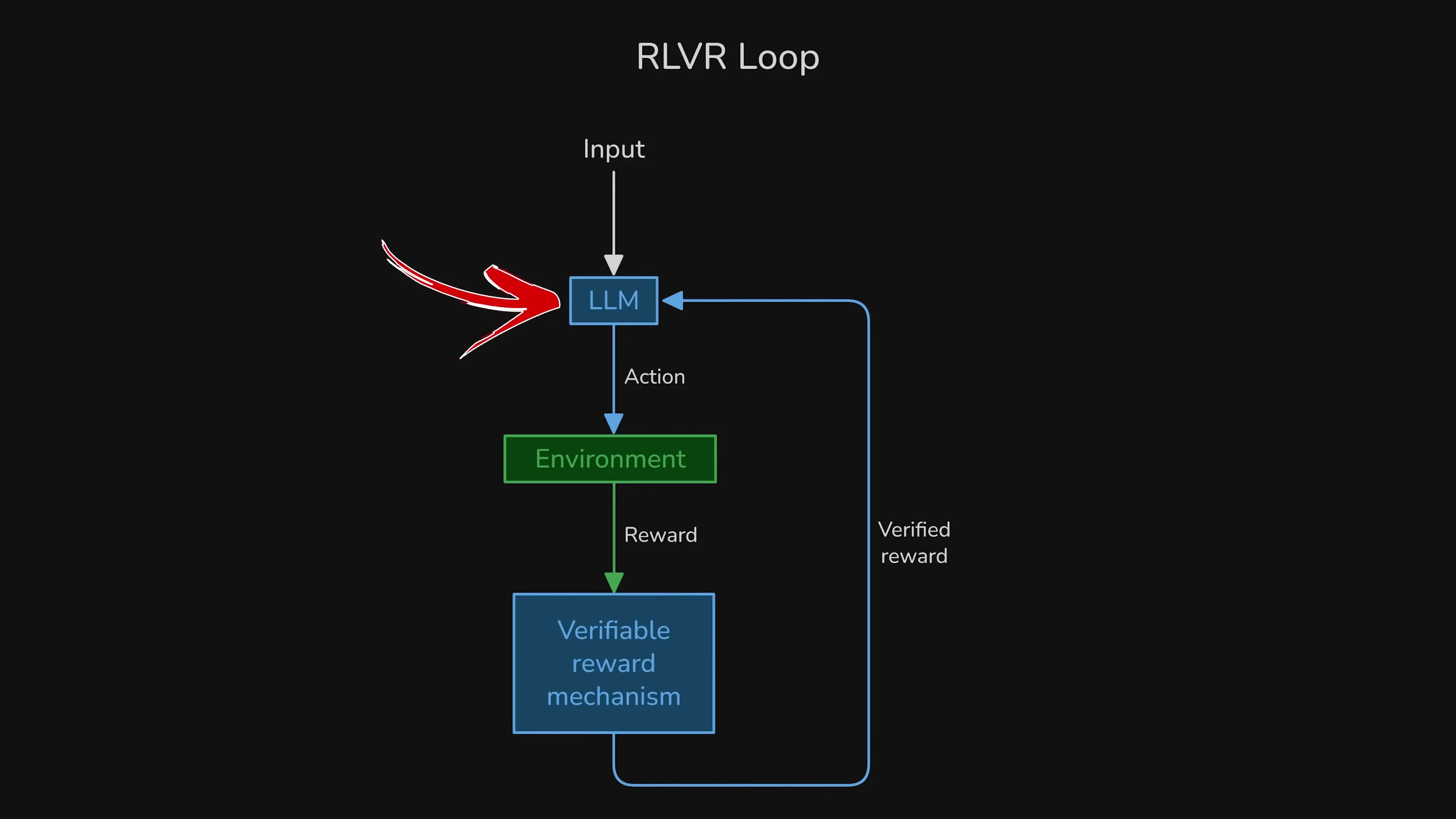
Reinforcement learning environments allow systematic verification of model behaviors

The core issue is that traditional RLVR provides only a binary reward signal (0 or 1) at the end of a potentially thousands-of-tokens-long generation process. This creates a diluted feedback signal where the model cannot determine which specific tokens were pivotal in determining the final outcome.

Entropy: The Key to Finding Pivotal Tokens

Researchers have discovered that entropy—a measure of uncertainty in probability distributions—can identify the crucial decision points in an LLM's token generation process. When an LLM predicts the next token, it assigns probabilities across its vocabulary (often 128K tokens). The entropy of this distribution reveals how certain or uncertain the model is about its prediction.

Mathematical formula for calculating entropy in token probability distributions

Entropy values in LLM token generation typically follow these patterns:

Less than 1 bit: The model is highly certain, with 90% probability on one token
1-3 bits: The model sees a small set of plausible continuations
Greater than 4 bits: The model has no strong preference, showing high uncertainty

Visualizations reveal that tokens with high entropy (often called "forking tokens") are typically followed by sequences of low-entropy tokens. This suggests that these high-entropy points are where the model makes critical decisions that determine the trajectory of what follows.

The 80/20 Rule: Focusing on What Matters

Researchers at Quinn explored a revolutionary idea: what if they simply stopped training on the 80% least uncertain tokens? In their paper "Beyond the 80/20 Rule," they implemented a system where tokens with entropy below the 80th percentile (specifically, less than 0.672 bits) would have their loss set to zero, providing no learning updates.

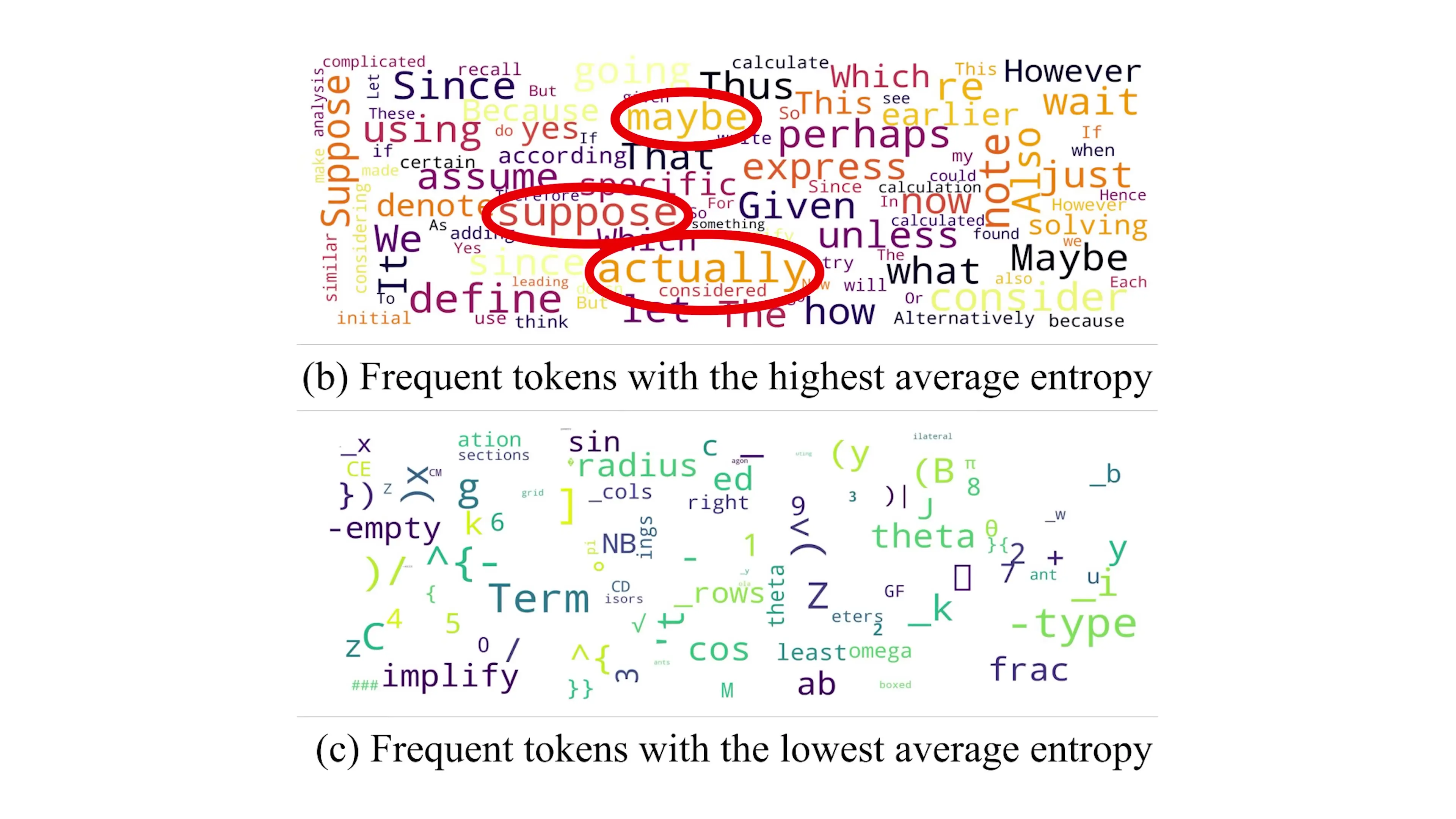
Examples of high-entropy tokens that represent critical decision points in language generation

This approach creates a clear distinction between high-entropy "forking tokens" (like "maybe," "actually," "suppose") and low-entropy tokens (like "radius," "Asian," "sin," and closing brackets). But does this distinction actually improve model performance?

Experimental Validation

To validate their hypothesis, the researchers conducted experiments with temperature settings—a hyperparameter controlling randomness in token sampling. They found that keeping non-forking tokens at a lower temperature than forking tokens consistently improved performance across benchmarks.

Most remarkably, when forking tokens were set at temperature 2 and non-forking tokens at temperature 1, the model outperformed the baseline. This confirmed that the model benefits when non-forking tokens are less random than forking tokens.

With this validation, Quinn researchers implemented a training approach that only updates the model on forking tokens. The results were remarkable:

80% reduction in backpropagation operations
Up to 50% reduction in total FLOPS (floating point operations)
7-11% accuracy improvement on AMY and math benchmarks for Quinn 332B

Amplifying Forking Tokens: An Alternative Approach

Rather than silencing non-forking tokens, another research paper titled "Reasoning with Exploration and Entropy Perspective" proposed amplifying the learning of forking tokens. This approach keeps feedback for all tokens but adds a bonus to tokens whose entropy rises above a moving baseline.

This technique turns each high-entropy token into a "tiny side quest" that encourages exploration. The process works through several steps:

During RLVR training, tokens with above-average entropy are marked as decision points
After grading, marked tokens receive a small bonus reward
This encourages the model to revisit uncertain spots and try different alternatives
Branches leading to correct answers receive continued bonuses and grow
Incorrect branches gradually shrink based on binary signals
Once a branch consistently succeeds, entropy drops below the threshold and exploration naturally decreases

The results show that while this approach initially underperforms the baseline (in the first 32 tries), it ultimately enables the model to solve more diverse problems over time (beyond 32 tries). This breaks the "shrinking behavior curves" often seen in standard RL methods, where models become more shallow and less creative over time.

Practical Implementation of Token-Level Entropy Analysis

For developers working with LLMs, implementing token-level entropy analysis requires access to the model's logits or probability distributions. Here's a simplified approach using Python and a common LLM tokenizer:

PYTHON

import numpy as np
from transformers import AutoTokenizer, AutoModelForCausalLM
import torch

# Load model and tokenizer
tokenizer = AutoTokenizer.from_pretrained("gpt2")
model = AutoModelForCausalLM.from_pretrained("gpt2")

# Calculate entropy for a given text
def calculate_token_entropy(text):
    inputs = tokenizer(text, return_tensors="pt")
    with torch.no_grad():
        outputs = model(**inputs, return_dict=True)
    
    # Get logits (unnormalized probabilities)
    logits = outputs.logits[0]
    
    # Convert to probabilities with softmax
    probs = torch.nn.functional.softmax(logits, dim=-1)
    
    # Calculate entropy: -sum(p * log(p))
    entropy = -torch.sum(probs * torch.log2(probs + 1e-10), dim=-1)
    
    # Get tokens
    tokens = tokenizer.convert_ids_to_tokens(inputs.input_ids[0])
    
    return list(zip(tokens, entropy.tolist()))

# Example usage
text = "The solution to this problem requires careful consideration."
token_entropies = calculate_token_entropy(text)

# Find high-entropy tokens (potential forking points)
high_entropy_tokens = [(token, entropy) for token, entropy in token_entropies 
                      if entropy > 2.0]  # Threshold can be adjusted

print("High entropy tokens (decision points):")
for token, entropy in high_entropy_tokens:
    print(f"Token: {token}, Entropy: {entropy:.2f} bits")

Implications for LLM Development

These entropy-based approaches to LLM training have profound implications for the field:

Computational efficiency: By focusing on high-entropy tokens, training requires significantly fewer resources
Improved reasoning: Models show better performance on complex tasks requiring multi-step reasoning
Enhanced diversity: Entropy-based exploration prevents models from collapsing to a single solution path
Better explainability: Identifying decision points helps understand how models reach conclusions
Targeted fine-tuning: Developers can focus optimization efforts on the tokens that matter most

Conclusion

Entropy-based token selection represents a significant advancement in LLM training methodology. By identifying and focusing on the critical decision points in token generation, researchers have found ways to dramatically improve model performance while reducing computational costs by up to 50%.

As this field continues to evolve, we can expect to see more sophisticated approaches to token-level optimization, potentially leading to more efficient, capable, and diverse language models. For developers and researchers working with LLMs, understanding token entropy provides a powerful tool for analyzing and improving model behavior.

How Entropy-Based Token Selection Revolutionizes Large Language Model Training