Why Gradient Descent Works Brilliantly in AI Despite Early Skepticism from Pioneers

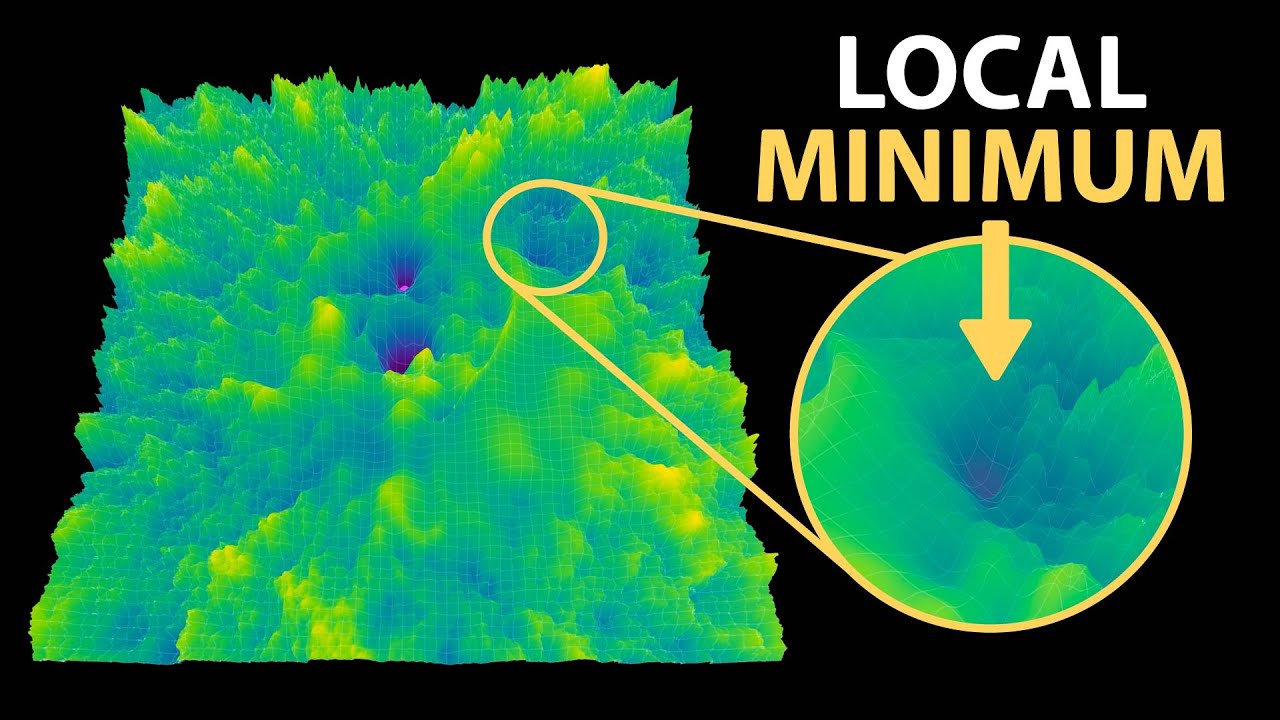
Gradient descent is the foundational optimization technique powering virtually all modern AI systems, including Meta's impressive Llama 3.2 large language model. Yet this seemingly straightforward approach—conceptualized as starting at a random point and moving downhill toward better solutions—was once considered fundamentally flawed by AI pioneers, including Geoffrey Hinton who would later win the 2024 Nobel Prize for his contributions to the field.

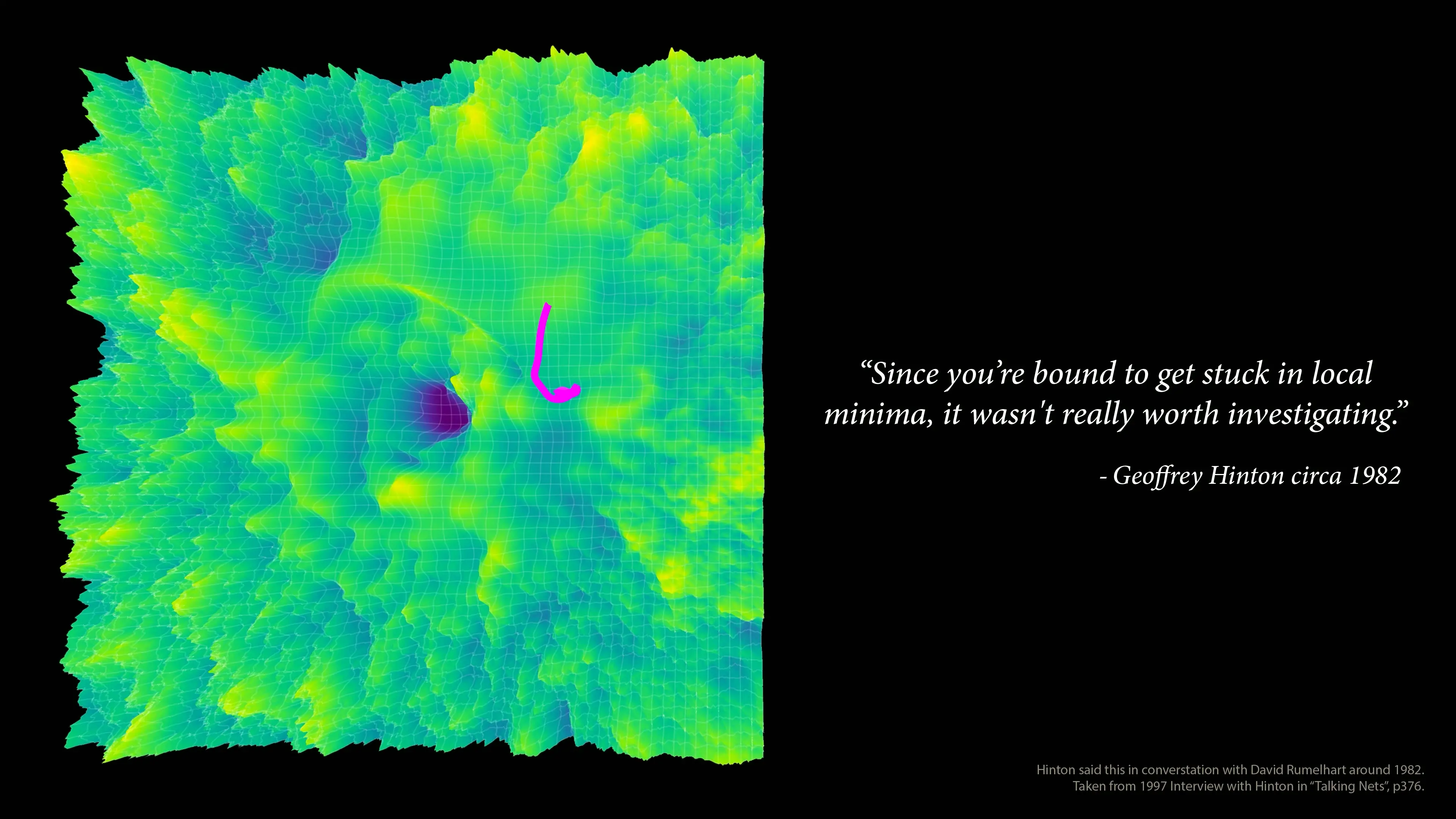
The Local Minima Problem That Almost Derailed AI

The fundamental concern that troubled early AI researchers was deceptively simple: how do neural networks avoid getting trapped in local minima—suboptimal solutions that appear optimal from a limited perspective? This question wasn't merely academic; it nearly stopped AI development in its tracks. Geoffrey Hinton himself initially rejected the possibility of effectively training neural networks using gradient descent specifically because of this theoretical limitation.

Yet today, gradient descent drives remarkably effective learning in models with billions of parameters. This apparent contradiction between theory and practice reveals a profound misunderstanding about how optimization actually works in high-dimensional spaces—a misconception that persisted for decades before being resolved by empirical success and deeper mathematical analysis.

How Large Language Models Actually Learn

To understand why gradient descent works so well in practice, we need to examine how models like Llama 3.2 actually process information and learn from data. At its core, a large language model takes a sequence of text, converts it into numerical tokens, and attempts to predict the next token in the sequence.

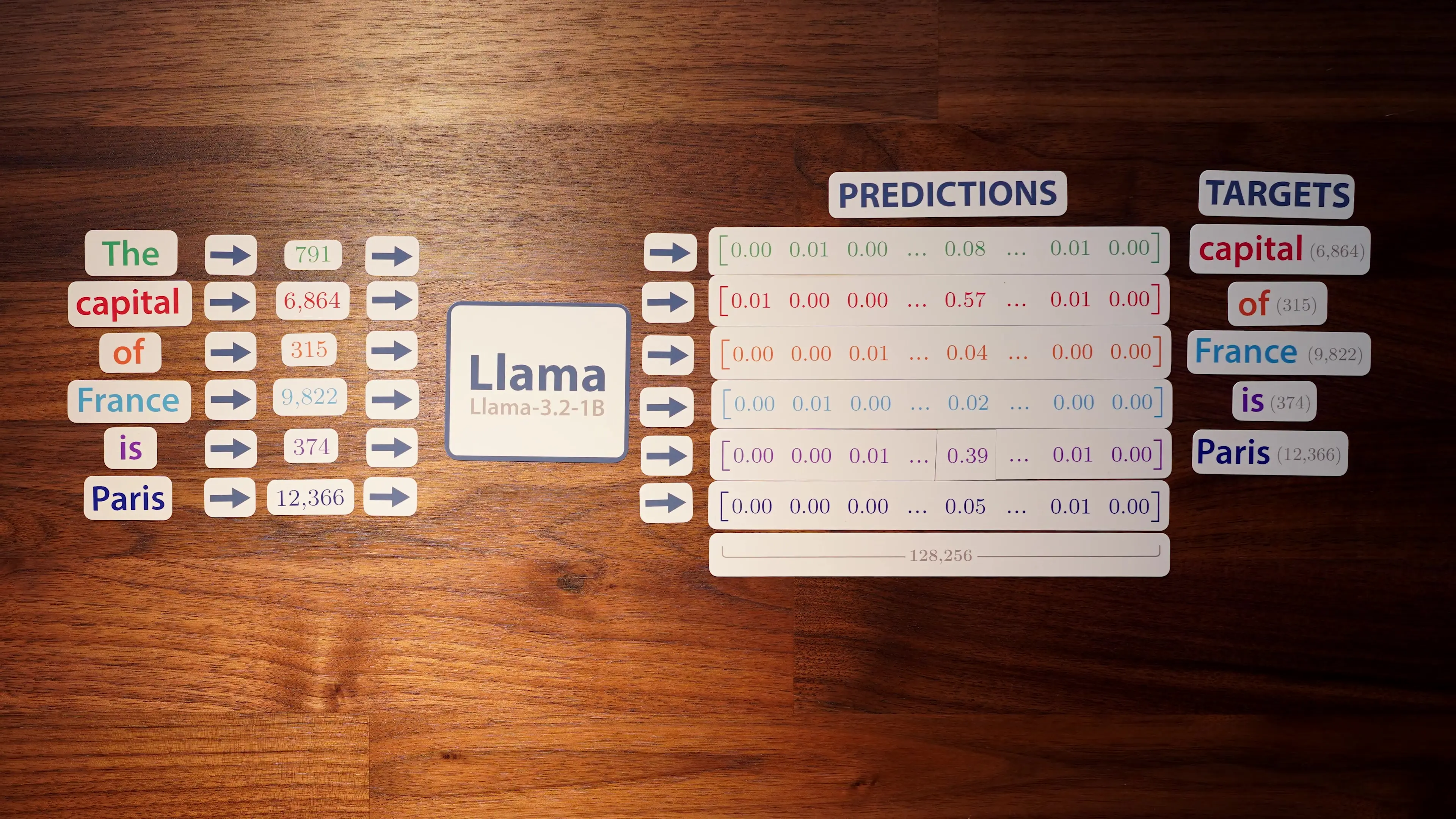
For example, when processing the phrase "The capital of France is," Llama 3.2 assigns a 39% probability to "Paris" as the next token, with lower probabilities to alternatives like "a" (8.4%). This probability distribution forms the foundation of how the model makes predictions and, crucially, how it learns through optimization.

Measuring and Optimizing Model Performance

To train a language model, we need a way to measure its performance. While we could simply calculate the error as one minus the probability assigned to the correct token (known as L1 loss), modern AI systems typically use cross-entropy loss instead. This function penalizes the model more severely as its confidence in the correct answer decreases, creating stronger learning signals.

• If the model assigns 100% probability to the correct token, the cross-entropy loss is 0
• At 90% probability, the loss is approximately 0.105
• At 80% probability, the loss increases to 0.223
• As confidence drops further, the loss grows exponentially

This loss function guides the entire learning process, as the model's parameters are adjusted to minimize this value across training examples.

The Wormhole Effect: Why Gradient Descent Isn't Just Going Downhill

The traditional visualization of gradient descent as simply moving downhill on a loss landscape fails to capture the true nature of optimization in high-dimensional spaces. In models like Llama 3.2 with 1.2 billion parameters, the process is more akin to falling through a wormhole than walking down a gentle slope.

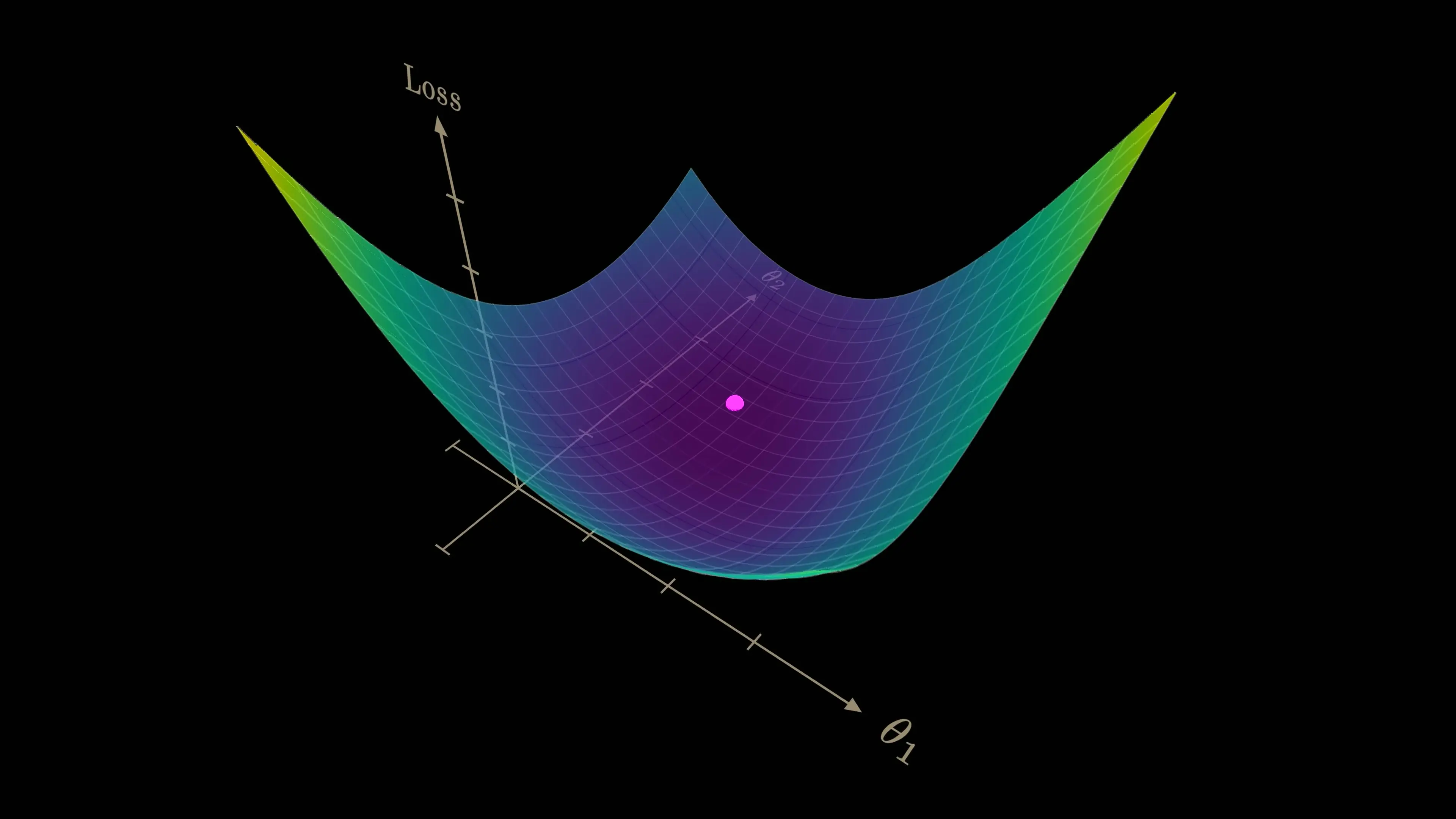
When we examine how individual parameters affect model performance, we discover complex interdependencies. Adjusting one parameter creates ripple effects throughout the network, dramatically changing how other parameters influence the output. This interconnected behavior means that optimizing parameters one-by-one is fundamentally impossible—the landscape itself shifts with each adjustment.

The Parameter Interdependency Challenge

Consider a single parameter in Llama's multi-layer perceptron block. Experiments show that adjusting this parameter creates a parabola-like curve in the model's output probability. While we might be tempted to set this parameter to its optimal value (around 1.61 in the example), doing so would change how all other parameters affect the output, essentially reshaping the entire optimization landscape.

This interdependency explains why local minima are far less problematic than early theorists feared. In high-dimensional spaces, true local minima are exceedingly rare—most apparent minima are actually saddle points with escape routes in other dimensions. The optimization process navigates these complex geometries through simultaneous adjustments to millions or billions of parameters.

Beyond Simple Visualizations: The Mathematics of High-Dimensional Learning

Our intuitive three-dimensional visualizations of loss landscapes fail to capture the true nature of learning in neural networks. In spaces with billions of dimensions, concepts like "downhill" become mathematically sophisticated and counterintuitive. The optimization process leverages mathematical properties unique to high-dimensional spaces that have no clear analogs in our everyday experience.

This explains why Hinton's initial concerns, while theoretically sound in low-dimensional spaces, don't apply to modern neural networks. The sheer dimensionality of parameter space creates optimization dynamics that early AI pioneers couldn't anticipate with the mathematical tools and computing resources available to them decades ago.

Practical Implications for AI Development

Understanding how gradient descent actually works in high-dimensional spaces has profound implications for AI development. It explains why scaling laws work—larger models with more parameters often train more efficiently and generalize better, despite having more complex loss landscapes. It also informs the design of optimization algorithms, learning rate schedules, and initialization strategies.

1. Modern optimizers like Adam and AdamW leverage the geometry of high-dimensional spaces
2. Learning rate schedules account for the changing nature of the loss landscape during training
3. Parameter initialization techniques prevent the model from starting in problematic regions
4. Regularization methods shape the loss landscape to improve generalization

Conclusion: The Unexpected Power of Gradient Descent

The journey from theoretical skepticism to practical success highlights an important lesson in artificial intelligence research: sometimes our intuitions about how algorithms should work fail to capture the true mathematical reality, especially in high-dimensional spaces. Gradient descent's remarkable effectiveness in training models like Llama 3.2 demonstrates that empirical results sometimes precede our theoretical understanding.

As we continue to develop more powerful AI systems, maintaining this balance between theoretical insights and practical experimentation will remain crucial. The story of gradient descent reminds us that sometimes the most powerful approaches are those that work in practice, even when our initial theoretical models suggest they shouldn't.